题目内容
 如图,点A是反比例函数y=-
如图,点A是反比例函数y=-| k |
| x |
| A、1 | B、3 | C、6 | D、-6 |
考点:反比例函数系数k的几何意义
专题:计算题
分析:作AE⊥BC于E,由四边形ABCD为平行四边形得AD∥x轴,则可判断四边形ADOE为矩形,所以S平行四边形ABCD=S矩形ADOE,根据反比例函数k的几何意义得到S矩形ADOE=|-k|,则|-k|=6,利用反比例函数图象得到-k<0,即k>0,于是有k=6.
解答:解: 作AE⊥BC于E,如图,
作AE⊥BC于E,如图,
∵四边形ABCD为平行四边形,
∴AD∥x轴,
∴四边形ADOE为矩形,
∴S平行四边形ABCD=S矩形ADOE,
而S矩形ADOE=|-k|,
∴|-k|=6,
而-k<0,即k>0,
∴k=6.
故选C.
 作AE⊥BC于E,如图,
作AE⊥BC于E,如图,∵四边形ABCD为平行四边形,
∴AD∥x轴,
∴四边形ADOE为矩形,
∴S平行四边形ABCD=S矩形ADOE,
而S矩形ADOE=|-k|,
∴|-k|=6,
而-k<0,即k>0,
∴k=6.
故选C.
点评:本题考查了反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
| k |
| x |
| k |
| x |

练习册系列答案
相关题目
小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,经过一段时间统计,他在路口遇到红灯的概率为
,遇到黄灯的概率为
,那么他遇到绿灯的概率为( )
| 1 |
| 4 |
| 1 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,AB=3,AC=
,BC=
,则tanA=( )
| 7 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如果某物体的三视图如图,那么该物体的形状是( )
如果某物体的三视图如图,那么该物体的形状是( )| A、正方体 | B、长方体 |
| C、三棱柱 | D、圆锥 |
把不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
 如图矩形AOBC,反比例函数图象y=
如图矩形AOBC,反比例函数图象y= 在?ABCD中,点E为AD的中点,连接BE,交AC于点F,AF=3,则AC=
在?ABCD中,点E为AD的中点,连接BE,交AC于点F,AF=3,则AC=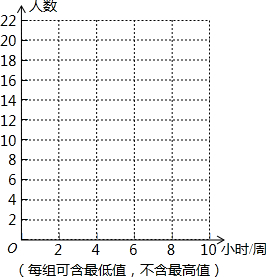 初三学生小英、小亮为了解本校820名初二学生每周体育锻炼的情况,各自在本校进行了抽样调查.小英调查了初二年级体育爱好者中40名学生每周体育锻炼的时间,算得这些学生平均每周锻炼时间为7.5小时;小亮从全体初二学生名单中随机抽取了40名学生,调查了他们每周锻炼的时间,算得这些学生平均每周锻炼时间为5.8小时.小英与小亮整理各自样本数据,如表所示.请根据上述信息,回答下列问题:
初三学生小英、小亮为了解本校820名初二学生每周体育锻炼的情况,各自在本校进行了抽样调查.小英调查了初二年级体育爱好者中40名学生每周体育锻炼的时间,算得这些学生平均每周锻炼时间为7.5小时;小亮从全体初二学生名单中随机抽取了40名学生,调查了他们每周锻炼的时间,算得这些学生平均每周锻炼时间为5.8小时.小英与小亮整理各自样本数据,如表所示.请根据上述信息,回答下列问题: