题目内容
11. 阅读理解:对于任意正实数a、b,∵$(\sqrt{a}-\sqrt{b})^{2}$≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,只有当a=b时,等号成立.
阅读理解:对于任意正实数a、b,∵$(\sqrt{a}-\sqrt{b})^{2}$≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,只有当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a、b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,只有当a=b时,a+b有最小值2$\sqrt{p}$.
根据上述内容,填空:若m>0,只有当m=2时,m+$\frac{4}{m}$有最小值,最小值为4.
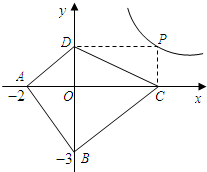
探索应用:如图,已知A(-2,0)、B(0,-3),P为双曲线y=$\frac{6}{x}$(x>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
实际应用:已知某汽车的一次运输成本包含以下三个部分:一是固定费用,共490元;二是燃油费,每千米为1.6元;三是折旧费,它与路程的平方成正比,比例系数为0.001.设该汽车一次运输的路程为x千米,求当x为多少时,该汽车平均每千米的运输成本最低?最低平均每千米的运输成本是多少元?
分析 阅读理解:根据提供的材料信息,先确定最小值,然后可得m的值;
探索应用:先表示出四边形ABCD的形状,然后再利用所给信息,求出最小值即可;
实际应用:表示出运输成本表达式,利用所给信息结论求出最低成本;
解答 解:阅读理解:由题意得:m+$\frac{4}{m}$≥2$\sqrt{m×\frac{4}{m}}$=4,当m=$\frac{4}{m}$时,取得最小值,
故若m>0,只有当m=2时,m+$\frac{4}{m}$有最小值,最小值为4;
探索应用:S四边形ABCD=S△BDA+S△BDC=$\frac{1}{2}$×2(x+3)+$\frac{1}{2}$x(x+3)=6+($\frac{3}{2}x$+$\frac{6}{x}$),
∵$\frac{3}{2}$x+$\frac{6}{x}$≥2$\sqrt{\frac{3}{2}x×\frac{6}{x}}$=6,
∴S四边形ABCD的最小值为12,
只有当$\frac{3}{2}$x=$\frac{6}{x}$时,取得最小值,此时x=2,
此时四边形ABCD是菱形;
实际应用:汽车平均每千米的运输成本=$\frac{490+1.6x+0.001{x}^{2}}{x}$=$\frac{490}{x}$+0.001x+1.6,
∵$\frac{490}{x}$+0.001x≥2$\sqrt{\frac{490}{x}×0.001x}$=1.4,
∴汽车平均每千米的运输成本最低是1.4+1.6=3元,
当$\frac{490}{x}$=0.001x,即x=700千米时,该汽车平均每千米的运输成本最低.
点评 本题考查了反比例函数的综合及二次根式的应用,读懂题目信息,理解阅读理解中的最小值的求法是解题的关键,难度一般,注意活学活用.

 一课一练课时达标系列答案
一课一练课时达标系列答案| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
| A. | 3,4,5 | B. | 5,6,9 | C. | 5,7,12 | D. | 5,8,10 |
| A. | 2≥x≥1 | B. | 1≤x<2 | C. | -1≤x<2 | D. | -2≤x<2 |
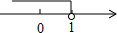 不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )
不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )| A. | a<1 | B. | a<2 | C. | a=1 | D. | a=2 |
 如图,过Rt△ABC的直角顶点C作直线CD∥AB,则图中与∠CAB互余的角共有( )
如图,过Rt△ABC的直角顶点C作直线CD∥AB,则图中与∠CAB互余的角共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
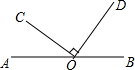 如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )| A. | 34° | B. | 44° | C. | 54° | D. | 64° |
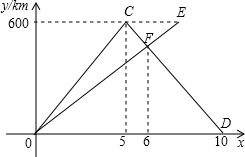 甲,乙两车同时从A城出发驶往B城,甲车到达B城后立即按原速返回A城,乙车继续行驶到B城,下面的图象反映的过程是离A城的距离y(km)与甲车行驶时间x(h)之间的函数关系.
甲,乙两车同时从A城出发驶往B城,甲车到达B城后立即按原速返回A城,乙车继续行驶到B城,下面的图象反映的过程是离A城的距离y(km)与甲车行驶时间x(h)之间的函数关系.