题目内容
 已知函数y=-
已知函数y=-| 1 |
| 2 |
| 3 |
| 2 |
(1)用配方法求它的顶点坐标;
(2)在平面直角坐标系中画出它的简图:
(3)根据图象回答:x取什么值时,y>0.
分析:(1)利用配方法步骤得出二次函数的顶点坐标即可;
(2)利用图象与x轴,y轴交点坐标以及顶点坐标,即可得出图象;
(3)利用函数图象,当函数大于0得出,x轴上方部分大于0,即可得出答案.
(2)利用图象与x轴,y轴交点坐标以及顶点坐标,即可得出图象;
(3)利用函数图象,当函数大于0得出,x轴上方部分大于0,即可得出答案.
解答: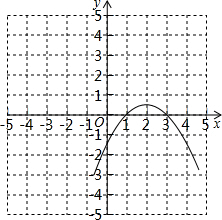 解:(1)y=-
解:(1)y=-
x2+2x-
,
=-
(x2-4x)-
,
=-
(x2-4x+4-4)-
,
=-
(x-2)2+
,
∴它的顶点坐标为:(2,
);
(2)∵二次函数的顶点坐标为:(2,
);
∴0=-
(x-2)2+
,
∴x=3或1,
∴图象与x轴交点坐标为(3,0),(1,0),
x=0,y=-
,
∴图象与y轴交点坐标为(0,-
),如图所示;
(3)利用函数大于0得出,x轴上方部分大于0,
∴当1<x<3时,y>0.
 解:(1)y=-
解:(1)y=-| 1 |
| 2 |
| 3 |
| 2 |
=-
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 1 |
| 2 |
| 1 |
| 2 |
∴它的顶点坐标为:(2,
| 1 |
| 2 |
(2)∵二次函数的顶点坐标为:(2,
| 1 |
| 2 |
∴0=-
| 1 |
| 2 |
| 1 |
| 2 |
∴x=3或1,
∴图象与x轴交点坐标为(3,0),(1,0),
x=0,y=-
| 3 |
| 2 |
∴图象与y轴交点坐标为(0,-
| 3 |
| 2 |
(3)利用函数大于0得出,x轴上方部分大于0,
∴当1<x<3时,y>0.
点评:此题主要考查了二次函数的性质以及配方法求二次函数的顶点坐标,利用数形结合得出图象在x轴上方部分y>0是解题关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 已知函数
已知函数 如图,已知函数
如图,已知函数