题目内容
如图10,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O的直经BD=6,连结CD、AO、BC,且AO与BC相交于点E。
(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(3)请阅读下方资源链接内容。
在(2)的基础上,若CD、AO的长
分别为一元二次方程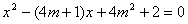 的两个实数根,求AB的长。
的两个实数根,求AB的长。
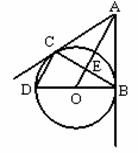
(1)证明:连接OC
∵AB、AC是⊙O的切线,∴∠ACO=∠ABO=90°
∵OC=OB,∴由HL可得 Rt△ACO≌Rt△ABO,∴AB=AC, ∠1=∠2
∴AE⊥BC, ∴∠AEC=90°
∵BD是⊙O的直径,∴∠DCB=90°, ∴∠DCB=∠AEC, ∴CD∥AO
(2)解:∵CD∥AO, ∴∠3=∠4
∵AB是⊙O的切线,DB是直径,∴∠DCB=∠ABO=90°
∴△BDC∽△AOB ∴ =
=  , ∴
, ∴ =
= , ∴y =
, ∴y = 
∵ ,∴自变量
,∴自变量 的取值范围为0<x<6 (3)解:∵CD、AO的长分别为一元二次方程
的取值范围为0<x<6 (3)解:∵CD、AO的长分别为一元二次方程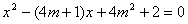 的两个实数根
的两个实数根
由求根公式可得,两根积为 ,
,
∴
又由(2)知y =  ,∴
,∴ ,∴
,∴ ,∴
,∴
①当 时,原方程可化为
时,原方程可化为 ,∴
,∴
由(2)知 ,∴只能取
,∴只能取
∴CD=3,AO=6,∴AB=
②当 时,原方程可化为
时,原方程可化为 ,
,
∵ ,∴方程无解
,∴方程无解
综上:AB的长为

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 一定经过点( ).
一定经过点( ). (0,k) D.(0,-1)
(0,k) D.(0,-1) 校园“阳光体育”工程,某校计划购买篮球和排球共20个.已知篮球每个80元,排球每个60元.设购买篮球x个,购买篮球和排球的总费用y元.
校园“阳光体育”工程,某校计划购买篮球和排球共20个.已知篮球每个80元,排球每个60元.设购买篮球x个,购买篮球和排球的总费用y元.
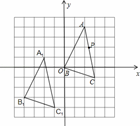
 的图象上,则y1、y2、y3的大小关系是( )
的图象上,则y1、y2、y3的大小关系是( )