Question

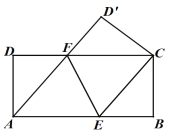
【题目】已知：如图，在中，，，，点为斜边的中点，以为圆心，5为半径的圆与相交于、两点，连结、．

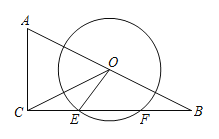
（1）求的长；

（2）求的正弦值．

Answer 1

【答案】（1）6；（2）．

【解析】

（1）过点O作OG⊥EF于点G，根据垂径定理得出EG=FG，然后由O为AB的中点，OG∥AC可推出OG为△ABC的中位线，从而可求出OG的长，在Rt△OEG中，由勾股定理可求出EG的长，从而可得出EF的长；

（2）首先由直角三角形斜边中线的性质可得出CO=BO，然后根据等腰三角形的性质可得出CG=BG，由（1）中EG=3可得，CE=5=OE，所以∠COE=∠OCE，在Rt△OCG中，求出sin∠OCG的值即可得出结果．

解：（1）过点O作OG⊥EF于点G，

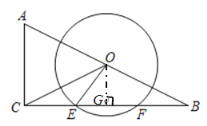
∴EG=FG，OG∥AC，

又O为AB的中点，∴G为BC的中点，即OG为△ABC的中位线，

∴OG=AC=4，

在Rt△OEG中，由勾股定理得，EG=，

∴EF=2EG=6；

（2）在Rt△ABC中，由勾股定理得，AB=，

又O为AB的中点，

∴CO=BO=4，又OG⊥BC，

∴CG=BG=BC=8，

∴CE=CG-EG=8-3=5，

∴CE=EO，

∴∠COE=∠OCE，

∴sin∠OCE=．

∴∠COE的正弦值为．