Question

【题目】已知：将矩形纸片ABCD折叠，使点A与点C重合（点D与D'为对应点），折痕为EF，连接AF.

（1）如图1，求证：四边形AECF为菱形；

（2）如图2，若FC=2DF，连接AC交EF于点O，连接DO、D'O，在不添加任何辅助线的情况下，请直接写出图2中所有等边三角形.

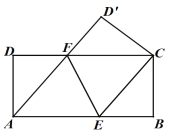
（图1） （图2）

Answer 1

【答案】（1）见解析（2）△AOD，△AEF，△CEF，△COD、

【解析】（1）先证明四边形AECF是平行四边形，再根据AE=CE，即可证明四边形AECF是菱形；

（2）根据等边三角形的判定方法可判定出等边三角形有△AEF、△CEF、△AOD、△COD′.

（1）∵将矩形纸片ABCD折叠，使点A与点C重合，折痕为EF，

∴AE=CE，AF=FC，∠AEF=∠CEF，

∵四边形ABCD是矩形，

∴∠ADC=∠BAD=90°，AE∥CF，

∴∠CFE=∠AEF，

∴∠CEF=∠CFE，

∴CF=CE，

∴AE=CF，

∴四边形AECF是平行四边形，

又∵AE=CE，

∴四边形AECF是菱形；

（2） 等边三角形为：△AEF、△CEF、△AOD、△COD′；理由如下：

∵FC=2DF，AF=FC，

∴AF=2DF，

∵∠ADC=90°，

∴∠DAF=30°，

∴∠EAF=60°，

∵四边形AECF是菱形，

∴AE=AF，△AEF≌△CEF，OA=OC=AC，

∴△AEF和△CEF是等边三角形；

∵∠ADC=90°，

∴OD=AC=OA，

∵∠OAF=∠EAF=30°，

∴∠OAD=60°，

∴△AOD是等边三角形；

∵CD′=AD=OC，OD′=AC，

∴CD′=OC=OD′，

∴△COD′是等边三角形．