Question

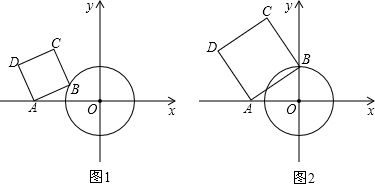
如图1，已知⊙O的半径长为3，点A是⊙O上一定点，点P为⊙O上不同于点A的动点．
（1）当时，求AP的长；
（2）如果⊙Q过点P、O，且点Q在直线AP上（如图2），设AP=x，QP=y，求y关于x的函数关系式，并写出函数的定义域；
（3）在（2）的条件下，当tanA=时（如图3），存在⊙M与⊙O相内切，同时与⊙Q相外切，且OM⊥OQ，试求⊙M的半径的长．

Answer 1

【答案】分析：（1）过点P作PB⊥OA交AO的延长线于B，连接OP，设PB=a，根据∠A的正切值表示出AB=2a，再表示出OE=2a-3，在Rt△POB中，利用勾股定理列方程求出a，然后在Rt△ABP中，利用勾股定理列式计算即可求出AP；
（2）连接OP、OQ，根据等边对等角可得∠P=∠POQ=∠A，求出△AOP和△PQO相似，利用相似三角形对应边成比例列式整理即可得到y与x的关系式，根据直径是圆的最长的弦写出x的取值范围；
（3）过点O作OC⊥AP于C，根据∠A的正切值，设OC=4b，则AC=3b，在Rt△AOC中，利用勾股定理列方程求出b，从而得到OC、AC，再根据等腰三角形三线合一的性质可得PC=AC，设⊙Q的半径为c，然后表示出CQ，在Rt△COQ中，利用勾股定理列方程求出c，设⊙M的半径为r，根据圆与圆的位置关系表示出MQ、MO然后利用勾股定理列方程求解即可得到r的值，从而得解．
解答：解：（1）如图1，过点P作PB⊥OA交AO的延长线于B，连接OP，设PB=a，
∵tanA=，
∴AB=2a，
∴OB=AB-OA=2a-3，
在Rt△POB中，PB²+OB²=OP²，
即a²+（2a-3）²=3²，
解得a₁=，a₂=0（舍去），
∴AB=2×=，
在Rt△ABP中，AP===；

（2）连接OP、OQ，则AO=PO，PQ=OQ，
∴∠P=∠A，∠POQ=∠P，
∴∠P=∠POQ=∠A，
∴△AOP∽△PQO，
∴=，
即=，
整理得，y=，
∵⊙O的半径为3，点P不同于点A，
∴0＜x≤6；
∴y=（0＜x≤6）；

（3）过点O作OC⊥AP于C，
∵tanA=，
∴设OC=4b，AC=3b，
在Rt△AOC中，OC²+AC²=OA²，
即（4b）²+（3b）²=3²，
解得b=，
∴OC=4×=，AC=3×=，
根据垂径定理，PC=AC=，
设⊙Q的半径为c，则CQ=QP-PC=c-，
在Rt△COQ中，OC²+CQ²=OQ²，
即（）²+（c-）²=c²，
解得c=，
设⊙M的半径为r，
∵⊙M与⊙O相内切，同时与⊙Q相外切，
∴MO=3-r，MQ=r+，
在Rt△OMQ中，MO²+OQ²=MQ²，
即（3-r）²+（）²=（r+）²，
解得r=．
点评：本题考查了圆的综合题型，主要利用了解直角三角形，勾股定理，同一个圆的半径相等，等边对等角的性质，相似三角形的判定与性质，圆与圆的位置关系，作辅助线构造出直角三角形与相似三角形是解题的关键，难点在于反复利用勾股定理列出方程求解．