��Ŀ����
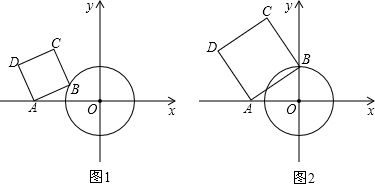
��ͼ1����֪��O�İ뾶Ϊ2����A������Ϊ��-4��0������BΪ��O�ϵĶ��㣬��ABΪ��������������ABCD��
��1������B��y�����������ʱ����ͼ2�����C�����꣮
��2����ֱ��AB���O����ʱ����ֱ��AB�Ľ���ʽ��
��3���趯��B�ĺ�����Ϊm��������ABCD�����ΪS�����S��m�ĺ�����ϵʽ�����ж�������ABCD������Ƿ�������ֵ����Сֵ��������ڣ����m��ֵ����������ڣ���˵�����ɣ�

��1������B��y�����������ʱ����ͼ2�����C�����꣮
��2����ֱ��AB���O����ʱ����ֱ��AB�Ľ���ʽ��
��3���趯��B�ĺ�����Ϊm��������ABCD�����ΪS�����S��m�ĺ�����ϵʽ�����ж�������ABCD������Ƿ�������ֵ����Сֵ��������ڣ����m��ֵ����������ڣ���˵�����ɣ�

��������1����ͼ2������C��CE��y���ڵ�E������ȫ�������Σ���ABO�ա�BCE��������ȫ�������εĶ�Ӧ�����֤��OB=EC=2��OA=EB=4����OE=OB+EB=6������C��-2��6����
��2����ͼ3������OB������B��BD��OA�ڵ�D���������ߵ�����֤�á�ABO=90�㣮ͨ����ֱ�ǡ�ABO��ֱ�ǡ�ABD������õ�B��������B��-1��
����Ȼ��ѵ�A��B������ֱ����ֱ��AB�ķ���
y=kx+b��k��0�����г�����k��b���ķ����飬ͨ���ⷽ���鼴��������ǵ�ֵ��
��3�����ɹ��ɶ������AB2=AD2+BD2=��4+m��2+4-m2=8m+20����S=8m+20�����Խ��ͼ�ο�֪-2��m��2����4��S��36������m=2ʱ��S���ֵ=36����m=-2ʱ��S��Сֵ=4��
��2����ͼ3������OB������B��BD��OA�ڵ�D���������ߵ�����֤�á�ABO=90�㣮ͨ����ֱ�ǡ�ABO��ֱ�ǡ�ABD������õ�B��������B��-1��
| 3 |
y=kx+b��k��0�����г�����k��b���ķ����飬ͨ���ⷽ���鼴��������ǵ�ֵ��
��3�����ɹ��ɶ������AB2=AD2+BD2=��4+m��2+4-m2=8m+20����S=8m+20�����Խ��ͼ�ο�֪-2��m��2����4��S��36������m=2ʱ��S���ֵ=36����m=-2ʱ��S��Сֵ=4��
��� �⣺��1����ͼ2���ߡ�O�İ뾶Ϊ2����A������Ϊ��-4��0�����ı���ABCD�������Σ�
�⣺��1����ͼ2���ߡ�O�İ뾶Ϊ2����A������Ϊ��-4��0�����ı���ABCD�������Σ�
��OA=4��OB=2��AB=BC����ABC=90�㣮
����C��CE��y���ڵ�E�����1=��2��ͬ�ŵ������ȣ���
���ڡ�ABO���BCE�У�
��
���ABO�ա�BCE��ASA����
��OB=EC=2��OA=EB=4��
��OE=OB+EB=2+4=6��
��C��-2��6����
��2����ͼ3������OB������B��BD��OA�ڵ�D��
��AB�ǡ�O�����ߣ�
���ABO=90�㣮
��OB=2��OA=4��
��OB=
OA��
���BAO=30�㣬
��AB=2
��
��BD=
��AD=3����OD=OA-AD=1��
��B��-1��
����
��ֱ��AB�Ľ���ʽΪ��y=kx+b��k��0������A��-4��0����B��-1��
�����룬��
��
��ã�
��
��ֱ��AB�Ľ���ʽΪ��y=
x+
��
��ֱ��AB����ֱ��AB����x��Գƣ�
��ֱ��AB��Ľ���ʽΪ��y=-
x-
��
��������������������ֱ��AB�ķ���Ϊy=
x+
��y=-
x-
��
��3��������ABCD������������ֵ����Сֵ���������£�
��ͼ3����ֱ�ǡ�OBD�У�OB=2��OD=|m|������ݹ��ɶ������BD2=OB2-OD2=4-m2��
��ֱ�ǡ�ABD�У����ݹ��ɶ������õ�AB2=AD2+BD2=��4+m��2+4-m2=8m+20����S=8m+20��
��-2��m��2��
��4��S��36������m=2ʱ��S���ֵ=36����m=-2ʱ��S��Сֵ=4��
����������S��m�ĺ�����ϵʽ��S=8m+20����m=2ʱ��S���ֵ=36����m=-2ʱ��S��Сֵ=4��
 �⣺��1����ͼ2���ߡ�O�İ뾶Ϊ2����A������Ϊ��-4��0�����ı���ABCD�������Σ�
�⣺��1����ͼ2���ߡ�O�İ뾶Ϊ2����A������Ϊ��-4��0�����ı���ABCD�������Σ���OA=4��OB=2��AB=BC����ABC=90�㣮
����C��CE��y���ڵ�E�����1=��2��ͬ�ŵ������ȣ���
���ڡ�ABO���BCE�У�
|
���ABO�ա�BCE��ASA����
��OB=EC=2��OA=EB=4��
��OE=OB+EB=2+4=6��
��C��-2��6����
��2����ͼ3������OB������B��BD��OA�ڵ�D��
��AB�ǡ�O�����ߣ�
���ABO=90�㣮
��OB=2��OA=4��
��OB=
| 1 |
| 2 |
���BAO=30�㣬
��AB=2
| 3 |
��BD=
| 3 |
��B��-1��
| 3 |
��ֱ��AB�Ľ���ʽΪ��y=kx+b��k��0������A��-4��0����B��-1��
| 3 |
|
��ã�
|

��ֱ��AB�Ľ���ʽΪ��y=
| ||
| 3 |
4
| ||
| 3 |
��ֱ��AB����ֱ��AB����x��Գƣ�
��ֱ��AB��Ľ���ʽΪ��y=-
| ||
| 3 |
4
| ||
| 3 |
��������������������ֱ��AB�ķ���Ϊy=
| ||
| 3 |
4
| ||
| 3 |
| ||
| 3 |
4
| ||
| 3 |
��3��������ABCD������������ֵ����Сֵ���������£�
��ͼ3����ֱ�ǡ�OBD�У�OB=2��OD=|m|������ݹ��ɶ������BD2=OB2-OD2=4-m2��
��ֱ�ǡ�ABD�У����ݹ��ɶ������õ�AB2=AD2+BD2=��4+m��2+4-m2=8m+20����S=8m+20��
��-2��m��2��
��4��S��36������m=2ʱ��S���ֵ=36����m=-2ʱ��S��Сֵ=4��
����������S��m�ĺ�����ϵʽ��S=8m+20����m=2ʱ��S���ֵ=36����m=-2ʱ��S��Сֵ=4��
�����������ۺϿ�����Բ�����ߵ����ʣ�����ϵ������һ�κ�������ʽ���������������֪ʶ�㣮����ʱ����������ˡ���ѧ��ϡ���ѧ˼������ƣ�ʹ�������������������������Ѷ����ݶȣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 3��˾���ڼ�ʻ����ʱ�����ֽ������������ɲ����Ҫһ��ʱ�䣬���ʱ��з�Ӧʱ�䣮֮�������ʻһ�ξ��룮���ǰ�˾���ӷ��ֽ������������ֹͣ����ʻ����ξ���С�ɲ�����롱����ͼ����
3��˾���ڼ�ʻ����ʱ�����ֽ������������ɲ����Ҫһ��ʱ�䣬���ʱ��з�Ӧʱ�䣮֮�������ʻһ�ξ��룮���ǰ�˾���ӷ��ֽ������������ֹͣ����ʻ����ξ���С�ɲ�����롱����ͼ����
 ˾���ڼ�ʻ����ʱ�����ֽ������������ɲ����Ҫһ��ʱ�䣬���ʱ��з�Ӧʱ�䣮֮�������ʻһ�ξ��룮���ǰ�˾���ӷ��ֽ������������ֹͣ����ʻ����ξ���С�ɲ�����롱����ͼ����
˾���ڼ�ʻ����ʱ�����ֽ������������ɲ����Ҫһ��ʱ�䣬���ʱ��з�Ӧʱ�䣮֮�������ʻһ�ξ��룮���ǰ�˾���ӷ��ֽ������������ֹͣ����ʻ����ξ���С�ɲ�����롱����ͼ����