题目内容
已知抛物线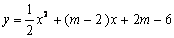 的对称轴为直线x=1,与x轴交于A,B 两点(点A在点B的左侧),与y轴交于点C.
的对称轴为直线x=1,与x轴交于A,B 两点(点A在点B的左侧),与y轴交于点C.
(1)求m的值;
(2)求A,B,C三点的坐标;
(3)过点C作直线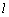 ∥x轴,将该抛物线在y轴左侧的部分沿直线
∥x轴,将该抛物线在y轴左侧的部分沿直线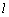 翻折,抛物线的其余部分保持不变,得到一个新的图象,记为G.请你结合图象回答:
翻折,抛物线的其余部分保持不变,得到一个新的图象,记为G.请你结合图象回答:
当直线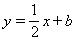 与图象G只有一个公共点时,求b的取值范围.
与图象G只有一个公共点时,求b的取值范围.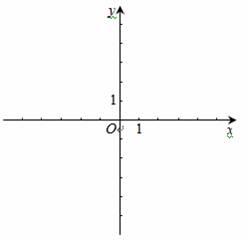
【试题解析】1)∵抛物线的对称轴为直线 ,
,
∴ .
.
∴ .
.
2)令 , ∴
, ∴
解得
∴
令 ,则
,则
∴
3)由图可知,
①当直线过 时,
时,
∴
②当直线与抛物线只有一个交点时,
∴
整理得
∵
∴
∴
结合函数图象可知, 的取值范围为
的取值范围为 或
或 .
.

练习册系列答案
相关题目




 ≈1.41,
≈1.41, ≈1.73)
≈1.73)

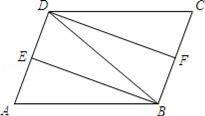
 中,AC﹦5,
中,AC﹦5, ,
, ,则
,则 B.12 C. 14 D.21
B.12 C. 14 D.21
 交折线 OAB 于点 E .
交折线 OAB 于点 E .