题目内容
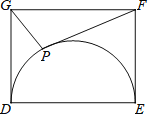
【题目】如图，在矩形
中， 
点
是
的中点，点
在
上，且
若在此矩形上存在一点
，使得
是等腰三角形，则点的个数是（ ）
A.
B.
C.
D.
【答案】D
【解析】
根据等腰三角形的定义，分三种情况讨论：①当
为腰，
为顶角顶点时，②当为腰，
为顶角顶点时，③当为底，
为顶角顶点时，分别确定点P的位置，即可得到答案．
∵在矩形
中，
，点是
的中点，
．
∴
是等腰三角形，存在三种情况：
①当为腰，为顶角顶点时，根据矩形的轴对称性，可知：在
上存在两个点P，在
上存在一个点P，共
个，使是等腰三角形；
②当为腰，为顶角顶点时，
在上存在一个点，使是等腰三角形；
③当为底，为顶角顶点时，点一定在的垂直平分线上，
∴的垂直平分线与矩形的交点，即为点，存在两个点．
综上所述，满足题意的点的个数是
．
故选
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
