题目内容
20.若$\sqrt{x-1}+\sqrt{3-x}$有意义,则1≤x≤3;若$\sqrt{x-1}+\root{3}{3-x}$有意义,则x≥1;若$\frac{\sqrt{x-1}}{3-x}$有意义,则x≥1且x≠3.分析 根据二次根式有意义的条件:被开方数是非负数,以及分母不能为0,即可解决问题.
解答 解:若$\sqrt{x-1}+\sqrt{3-x}$有意义,则$\left\{\begin{array}{l}{x-1≥0}\\{3-x≥0}\end{array}\right.$解得1≤x≤3.
若$\sqrt{x-1}+\root{3}{3-x}$有意义,则x-1≥0,x≥1.
若$\frac{\sqrt{x-1}}{3-x}$有意义,则$\left\{\begin{array}{l}{x-1≥0}\\{3-x≠0}\end{array}\right.$,解得x≥1且x≠3.
故答案分别为1≤x≤3;x≥1;x≥1且x≠3.
点评 本题考查二次根式有意义的条件,掌握二次根式的被开方数是非负数这个条件以及分母不能为0,任何实数都有立方根,属于中考常考题型.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
11.函数y=$\frac{x+3}{\sqrt{x-2}}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x>2且x≠-3 | C. | x>-3 | D. | x≥-3且x≠2 |
 定义:将一个图形L沿某个方向平移一段距离后,该图形在平面上留下的痕迹称之为图形L在该方向的拖影.如图,四边形ABB′A′是线段AB水平向右平移得到的拖影.则将下面四个图形水平向右平移适当距离,其拖影是五边形的是( )
定义:将一个图形L沿某个方向平移一段距离后,该图形在平面上留下的痕迹称之为图形L在该方向的拖影.如图,四边形ABB′A′是线段AB水平向右平移得到的拖影.则将下面四个图形水平向右平移适当距离,其拖影是五边形的是( )



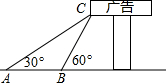 如图,某校数学兴趣小组为了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到点B处,又测得C点的仰角为60°.请你根据以上数据求C点离地面的高度(结果保留根号).
如图,某校数学兴趣小组为了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到点B处,又测得C点的仰角为60°.请你根据以上数据求C点离地面的高度(结果保留根号).
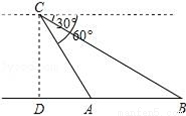
 上,且x1<x2<0<x3,则下列各式正确的是( )
上,且x1<x2<0<x3,则下列各式正确的是( )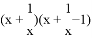 =2,则
=2,则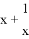 =______.
=______.