题目内容
15.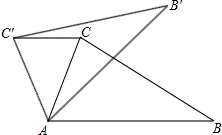 如图,在△ABC中,∠CAB=80°.在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=20°.
如图,在△ABC中,∠CAB=80°.在同一平面内,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′=20°.
分析 旋转中心为点A,B与B′,C与C′分别是对应点,根据旋转的性质可知,旋转角∠BAB′=∠CAC′,AC=AC′,再利用平行线的性质得∠C′CA=∠CAB,把问题转化到等腰△ACC′中,根据内角和定理求∠CAC′,即可求出∠BAB′的度数.
解答 解:∵CC′∥AB,∠CAB=80°,
∴∠C′CA=∠CAB=80°,
又∵C、C′为对应点,点A为旋转中心,
∴AC=AC′,即△ACC′为等腰三角形,
∴∠BAB′=∠CAC′=180°-2∠C′CA=20°,
故答案为:20.
点评 本题考查了旋转的基本性质,对应点到旋转中心的距离相等,对应点与旋转中心的连线的夹角为旋转角.同时考查了平行线的性质.

练习册系列答案
相关题目
16.下列二次根式与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{0.2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{50}$ |
17.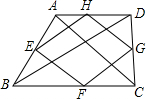 如图,顺次连接四边形ABCD各边中点,得到四边形EFGH,在下列条件中可使四边形EFGH为菱形的是( )
如图,顺次连接四边形ABCD各边中点,得到四边形EFGH,在下列条件中可使四边形EFGH为菱形的是( )
 如图,顺次连接四边形ABCD各边中点,得到四边形EFGH,在下列条件中可使四边形EFGH为菱形的是( )
如图,顺次连接四边形ABCD各边中点,得到四边形EFGH,在下列条件中可使四边形EFGH为菱形的是( )| A. | AB=CD | B. | AC=BD | C. | AC丄BD | D. | AD∥BC |
7.当k>0,y<0时,反比例函数y=$\frac{k}{x}$的图象在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在数轴上点A和点B之间的整数是-1、0、1、2.
如图,在数轴上点A和点B之间的整数是-1、0、1、2.