题目内容
(本题满分10分)在平面直角坐标系中,点A的坐标为(-6, 6),以A为顶点的∠BAC的两边始终与x轴交于B、C两点(B在C左面),且∠BAC=45°.
(1)如图,连接OA,当AB=AC时,试说明:OA=OB.

(2)过点A作AD⊥x轴,垂足为D,当DC=2时,将∠BAC沿AC所在直线翻折,翻折后边AB交y轴于点M,求点M的坐标.


(1)见解析;(2)M点坐标为(0,3)或M点坐标为(0,—6).
【解析】
试题分析:(1)根据题目中角的度数,求出∠BAO=∠ABC=67.5°,利用等腰三角形的性质即可得出结论;
(2)根据题意,可知要分两种情况,即当点C在点D右侧时或当点C在点D左侧时,利用勾股定理即可得出M点坐标.
试题解析:
(1)∵AB=AC,∠BAC=45°,∴∠ABC=∠ACB= 67.5°.
过点A作AE⊥OB于E,则△AEO是等腰直角三角形,∠EAO=45°.
∵AB=AC,AE⊥OB,
∴∠BAE=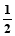 ∠BAC=22.5°.
∠BAC=22.5°.
∴∠BAO=67.5°=∠ABC
∴OA=OB,
(2)设OM=x.
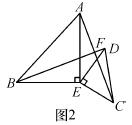
当点C在点D右侧时,连接CM,过点A作AF⊥y轴于点F,
由∠BAM=∠DAF=90°可知:∠BAD=∠MAF;
∵AD=AF=6,∠BDA=∠MFA=90°,
∴△BAD≌△MAF.
∴BD=FM=6—x.
∵AC=AC,∠BAC=∠MAC,
∴△BAC≌△MAC.
∴BC=CM=8—x.
在Rt△COM中,由勾股定理得:OC2+OM2=CM2,即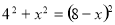 ,
,
解得:x=3,∴M点坐标为(0,3).
当点C在点D左侧时,连接CM,过点A作AF⊥y轴于点F,
同理,△BAD≌△MAF,∴BD=FM=6+x.
同理,△BAC≌△MAC,∴BC=CM=4+x.
在Rt△COM中,由勾股定理得:OC2+OM2=CM2,即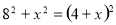 ,
,
解得:x=6,∴M点坐标为(0,—6)

考点:等腰三角形的性质;翻折的性质.

 名校课堂系列答案
名校课堂系列答案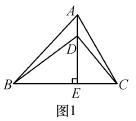
 B.-
B.- .
.
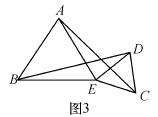
 ,点D在BC边上,连接AD,若tan∠CAD=
,点D在BC边上,连接AD,若tan∠CAD= ,则BD的长为 .
,则BD的长为 .