题目内容
三角形ABC是等腰三角形,AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕CE,求三角形ACE的面积.
分析:要求三角形ACE的面积,则必须求得一边及对应的高,由已知的条件及折叠的性质,根据勾股定理很容易求得.
解答: 解:在△ABC中,
解:在△ABC中,
∵AB=AC AD⊥BC BC=10,
∴BD=DC=
,BC=5 (2分)
在Rt△ACD中AC=13,CD=5
由勾股定理得:
AD=
=
=12 (4分)
由对折性质知:△CDE≌△CFE
∴CF=CD=5 DE=EF,
∴AF=13-5=8,(5分)
设DE=x=EF,则AE=12-x (6分)
在Rt△AEF中由勾股定理得:
AE2=EF2+AF2,即(12-x)=x+82,整理得,104-24x+x2=x2+64,即24x=80,解得x=
(8分)
∴S△ACE=
AC•EF=
×13×
=
(9分)
答:三角形ACE的面积是
平方单位. (16分)
 解:在△ABC中,
解:在△ABC中,∵AB=AC AD⊥BC BC=10,
∴BD=DC=
| 1 |
| 2 |
在Rt△ACD中AC=13,CD=5
由勾股定理得:
AD=
| AC2-CD2 |
| 132-52 |
由对折性质知:△CDE≌△CFE
∴CF=CD=5 DE=EF,
∴AF=13-5=8,(5分)
设DE=x=EF,则AE=12-x (6分)
在Rt△AEF中由勾股定理得:
AE2=EF2+AF2,即(12-x)=x+82,整理得,104-24x+x2=x2+64,即24x=80,解得x=
| 10 |
| 3 |
∴S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
| 3 |
| 65 |
| 3 |
答:三角形ACE的面积是
| 65 |
| 3 |
点评:本题考查的是翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,注意思维要围绕折叠的性质解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

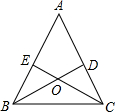 如图,△ABC中,D、E分别是AC,AB上的点,BD与CE交于点O,给出下列三个条件:①BE=CD;②∠BCE=∠CBD;③BD=CE.请在上述三个条件中选取两个合适的条件来判定△ABC是等腰三角形.
如图,△ABC中,D、E分别是AC,AB上的点,BD与CE交于点O,给出下列三个条件:①BE=CD;②∠BCE=∠CBD;③BD=CE.请在上述三个条件中选取两个合适的条件来判定△ABC是等腰三角形.