题目内容
(2013•济宁三模)如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.

(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.求证:BD⊥CF;
(3)在(2)小题的条件下,AC与BG的交点为M,当AB=4,AD=
时,求线段CM的长.

(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.求证:BD⊥CF;
(3)在(2)小题的条件下,AC与BG的交点为M,当AB=4,AD=
| 2 |
分析:(1)根据△ABC是等腰直角三角形,四边形ADEF是正方形,根据角边角关系证出△BAD≌△CAF,根据全等三角形的对应边相等,即可证得BD=CF;
(2)先设BG交AC于点M,根据(1)证出的△BAD≌△CAF,可得∠ABM=∠GCM,又根据对顶角相等,得出△BMA∽△CMG,再根据根据相似三角形的对应角相等,可得∠BGC=∠BAC=90°,即可证出BD⊥CF;
(3)首先过点F作FN⊥AC于点N,利用勾股定理即可求得AE,BC的长,继而求得AN,CN的长,又由等角的三角函数值相等,可求得AM的值,从而求出CM的值.
(2)先设BG交AC于点M,根据(1)证出的△BAD≌△CAF,可得∠ABM=∠GCM,又根据对顶角相等,得出△BMA∽△CMG,再根据根据相似三角形的对应角相等,可得∠BGC=∠BAC=90°,即可证出BD⊥CF;
(3)首先过点F作FN⊥AC于点N,利用勾股定理即可求得AE,BC的长,继而求得AN,CN的长,又由等角的三角函数值相等,可求得AM的值,从而求出CM的值.
解答: (1)解:BD=CF成立.
(1)解:BD=CF成立.
理由:∵△ABC是等腰直角三角形,四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∵∠BAD=∠BAC-∠DAC,∠CAF=∠DAF-∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,
,
∴△BAD≌△CAF(SAS),
∴BD=CF.
(2)证明:设BG交AC于点M,
∵△BAD≌△CAF,
∴∠ABM=∠GCM,
∵∠BMA=∠CMG,
∴△BMA∽△CMG,
∴∠BGC=∠BAC=90°,
∴BD⊥CF.
(3)过点F作FN⊥AC于点N,
∵在正方形ADEF中,AD=DE=
,
∴AE=
=2,
∴AN=FN=
AE=1.
∵在等腰直角△ABC中,AB=AC=4,
∴CN=AC-AN=3,BC=
=4
,
∴在Rt△FCN中,tan∠FCN=
=
,
∴在Rt△ABM中,tan∠ABM
=tan∠FCN=
,
∴AM=
AB=
,
∴CM=AC-AM=4-
=
.
 (1)解:BD=CF成立.
(1)解:BD=CF成立.理由:∵△ABC是等腰直角三角形,四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∵∠BAD=∠BAC-∠DAC,∠CAF=∠DAF-∠DAC,
∴∠BAD=∠CAF,
∵在△BAD和△CAF中,
|
∴△BAD≌△CAF(SAS),
∴BD=CF.
(2)证明:设BG交AC于点M,
∵△BAD≌△CAF,
∴∠ABM=∠GCM,
∵∠BMA=∠CMG,
∴△BMA∽△CMG,
∴∠BGC=∠BAC=90°,
∴BD⊥CF.
(3)过点F作FN⊥AC于点N,
∵在正方形ADEF中,AD=DE=
| 2 |
∴AE=
| AD2+DE2 |
∴AN=FN=
| 1 |
| 2 |
∵在等腰直角△ABC中,AB=AC=4,
∴CN=AC-AN=3,BC=
| AB2+AC2 |
| 2 |
∴在Rt△FCN中,tan∠FCN=
| FN |
| CN |
| 1 |
| 3 |
∴在Rt△ABM中,tan∠ABM
| AM |
| AB |
| 1 |
| 3 |
∴AM=
| 1 |
| 3 |
| 4 |
| 3 |
∴CM=AC-AM=4-
| 4 |
| 3 |
| 8 |
| 3 |
点评:此题考查了四边形的综合,用到的知识点是相似三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的性质、矩形的性质、勾股定理以及三角函数等知识,此题综合性很强,难度较大,注意数形结合思想应用.

练习册系列答案
相关题目
 (2013•济宁三模)如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.
(2013•济宁三模)如图,已知直线y=kx-6与抛物线y=ax2+bx+c相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上.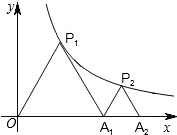 (2013•济宁三模)如图,P1是反比例函数y=
(2013•济宁三模)如图,P1是反比例函数y=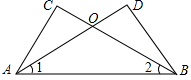 (2013•济宁三模)(1)一个人由山底爬到山顶,需先爬45°的山坡200m,再爬30°的山坡300m,求山的高度(结果可保留根号).
(2013•济宁三模)(1)一个人由山底爬到山顶,需先爬45°的山坡200m,再爬30°的山坡300m,求山的高度(结果可保留根号).