题目内容

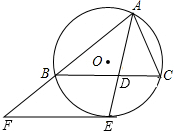
（人教版）已知：如图，AB=BC，∠ABC=90°，以AB为直径的⊙O交OC于点D，AD的延长线交BC于点E，过D作⊙O的切线交BC于点F．下列结论：①CD2=CE•CB；②4EF2=ED•EA；③∠OCB=∠EAB；④DF=
1
2
CD．其中正确的有（　　）
A．①②③B．②③④C．①③④D．①②④

连接BD，可得△CDE∽△CBD，
∴CD2=CE•CB，
还可得出EF=FB，EB2=ED•EA，
EB=2EF，
∴4EF2=ED•EA，
∵△CDF∽△CBO，
∴
DF
BO
=
CD
CB
，
∴
DF
CD
=
BO
CB
=
1
2
，
∴DF=
1
2
CD．
综上正确的有①、②、④．
故选D．
练习册系列答案
相关题目
已知：射线OF交⊙O于点B，半径OA⊥OB，P是射线OF上的一个动点（不与O、B重合），直线AP交⊙O于D，过D作⊙O的切线交射线OF于E．
（1）图a是点P在圆内移动时符合已知条件的图形，请你在图b中画出点P在圆外移动时符合已知条件的图形；
（2）观察图形，点P在移动过程中，△DPE的边、角或形状存在某些规律，请你通过观察、测量、比较，写出一条与△DPE的边、角或形状有关的规律；
（3）在点P移动过程中，设∠DEP的度数为x，∠OAP的度数为y，求y与x的函数关系式，并写出自变量x的取值范围．
如图，已知：在直角坐标系中．点E从O点出发，以1个单位/秒的速度沿x轴正方向运动，点F从O点出发，以2个单位/秒的速度沿y轴正方向运动．B（4，2），以BE为直径作⊙O1．

（1）若点E、F同时出发，设线段EF与线段OB交于点G，试判断点G与⊙O1的位置关系，并证明你的结论；
（2）在（1）的条件下，连接FB，几秒时FB与⊙O1相切？
（3）若点E提前2秒出发，点F再出发．当点F出发后，点E在A点的左侧时，设BA⊥x轴于点A，连接AF交⊙O1于点P，试问AP•AF的值是否会发生变化？若不变，请说明理由并求其值；若变化，请求其值的变化范围．
设计一把直尺ABC，BC在地面上，AB与地面垂直，并且AB=10cm，移动一个半径不小于10cm的圆形轮子，使轮子紧靠A点，且与BC相切于D点（如图）．设计要求在D处的刻度恰好显示这个轮子的半径（以厘米为单位）．那么，当BC的长度为1M时，BC上可标出的最大刻度是______．
如图，在Rt△ABC中，∠C=90°，点O在AB上，以O为圆心，OA长为半径的圆与AC、AB分别交于D、E，且⊙O与直线BD刚好相切．
（1）试证：∠CBD=∠A；
（2）若cosA=
2
5
5
，BD=2
5
，试计算⊙O的面积．
如图，A、B是⊙O上的两点，AC是⊙O的切线，∠OBA=75°，⊙O的半径为1，则OC的长等于（　　）
A．
3
2
B．
2
2
C．
2
3
3
D．
2
如图，点A、B、C分别是⊙O上的点，∠B=60°，CD是⊙O的直径，P是CD延长线上的点，且AP=AC．
（1）求证：AP是⊙O的切线；
（2）若AC=3，求PD的长．
如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠A=36°，则∠C=______．
在△ABC中，∠BAC的平分线AD交△ABC的外接圆⊙O于点E，交BC于点D，过点E作⊙O的切线交AB的延长线于点F，若AD=3
3
，DE=
3
．
求证：
（1）EF∥BC；
（2）AF=2EF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网