题目内容
在△ABC中，∠BAC的平分线AD交△ABC的外接圆⊙O于点E，交BC于点D，过点E作⊙O的切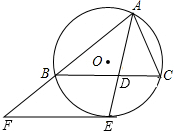
线交AB的延长线于点F，若AD=3
，DE=
．
求证：
（1）EF∥BC；
（2）AF=2EF．
线交AB的延长线于点F，若AD=3| 3 |
| 3 |
求证：
（1）EF∥BC；
（2）AF=2EF．
证明：（1）连接OE．
∵EF切⊙O于点E，则OE⊥EF．
∵AE平分∠BAC，∴
=
．
∴OE⊥BC．
∴EF∥BC．
（2）∵EF∥BC，AD=3
，DE=
．
∴AD：DE=AB：BF=3：1．
∴BF=
AF．
∵FE是切线，FA是割线，
∴EF2=FB•FA=
FA2，
∴EF=
FA，即AF=2EF．
∵EF切⊙O于点E，则OE⊥EF．
∵AE平分∠BAC，∴
 |
| BE |
|
| EC |
∴OE⊥BC．
∴EF∥BC．
（2）∵EF∥BC，AD=3
| 3 |
| 3 |
∴AD：DE=AB：BF=3：1．
∴BF=
| 1 |
| 4 |
∵FE是切线，FA是割线，
∴EF2=FB•FA=
| 1 |
| 4 |
∴EF=
| 1 |
| 2 |
练习册系列答案
名校课堂系列答案
相关题目
点D，作CE⊥OB于点E，点M在DE上，DM=2EM，过点C的直线PC交OA的延长线于点P，且∠CPD=∠CDE．
