题目内容
如图1,在⊙O中,E是弧AB的中点,C为⊙O上的一动点(C与E在AB异侧),连接EC交AB于点F,EB= (r是⊙O的半径).
(r是⊙O的半径).
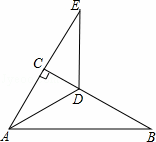
(1)D为AB延长线上一点,若DC=DF,证明:直线DC与⊙O相切;
(2)求EF•EC的值;
(3)如图2,当F是AB的四等分点时,求EC的值.

(1)证明:连结OC、OE,OE交AB于H,如图1,
∵E是弧AB的中点,
∴OE⊥AB,
∴∠EHF=90°,
∴∠HEF+∠HFE=90°,
而∠HFE=∠CFD,
∴∠HEF+∠CFD=90°,
∵DC=DF,
∴∠CFD=∠DCF,
而OC=OE,
∴∠OCE=∠OEC,
∴∠OCE+∠DCE=∠HEF+∠CFD=90°,
∴OC⊥CD,
∴直线DC与⊙O相切;
(2)解:连结BC,
∵E是弧AB的中点,
∴弧AE=弧BE,
∴∠ABE=∠BCE,
而∠FEB=∠BEC,
∴△EBF∽△ECB,
∴EF:BE=BE:EC,
∴EF•EC=BE2=( r)2=
r)2= r2;
r2;
(3)解:如图2,连结OA,
∵弧AE=弧BE,
∴AE=BE= r,
r,
设OH=x,则HE=r﹣x,
在Rt△OAH中,AH2+OH2=OA2,即AH2+x2=r2,
在Rt△EAH中,AH2+EH2=EA2,即AH2+(r﹣x)2=( r)2,
r)2,
∴x2﹣(r﹣x)2=r2﹣( r)2,即得x=
r)2,即得x= r,
r,
∴HE=r﹣ r=
r= r,
r,
在Rt△OAH中,AH= =
= =
= ,
,
∵OE⊥AB,
∴AH=BH,
而F是AB的四等分点,
∴HF= AH=
AH= ,
,
在Rt△EFH中,EF= =
= =
= r,
r,
∵EF•EC= r2,
r2,
∴ r•EC=
r•EC= r2,
r2,
∴EC= r.
r.



如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,下列说法不正确的是( )

|
| A. | △CDF的周长等于AD+CD | B. | FC平分∠BFD |
|
| C. | AC2+BF2=4CD2 | D. | DE2=EF•CE |
下列说法正确的是( )
|
| A. | “打开电视机,它正在播广告”是必然事件 |
|
| B. | “一个不透明的袋中装有8个红球,从中摸出一个球是红球”是随机事件 |
|
| C. | 为了了解我市今年夏季家电市场中空调的质量,不宜采用普查的调查方式进行 |
|
| D. | 销售某种品牌的凉鞋,销售商最感兴趣的是该品牌凉鞋的尺码的平均数 |
 ,其中a=﹣1.
,其中a=﹣1. 中,自变量x的取值范围是
中,自变量x的取值范围是  B.
B.  C.
C.  D.
D. 
