题目内容
如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB．
（1）求∠CAD的度数；
（2）延长AC至E，使CE=AC，求证：DA=DE．
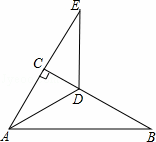
（1）解
：如图，∵在Rt△ABC中，∠ACB=90°，∠B=30°，
∴∠B=30°，
∴∠CAB=60°．
又∵AD平分∠CAB，
∴∠CAD=
∠CAB=30°，即∠CAD=30°；
（2）证明：∵∠ACD+∠ECD=180°，且∠ACD=90°，
∴∠ECD=90°，
∴∠ACD=∠ECD．
在△ACD与△ECD中，
，
∴△ACD≌△ECD（SAS），
∴DA=DE．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知三角形两边长分别为3和8，则该三角形第三边的长可能是（ ）
|
| A． | 5 | B． | 10 | C． | 11 | D． | 12 |
如图，在4×4的正方形网格中，每个小正方形的边长为1，若将△AOC绕点O顺时针旋转90°得到△BOD，则
的长为（ ）
|
| A． | π | B． | 6π | C． | 3π | D． | 1.5π |
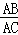=a，点G，H分别在边AB，DC上，且HA=HG，点E为AB边上的一个动点，连接HE，把△AHE沿直线HE翻折得到△FHE．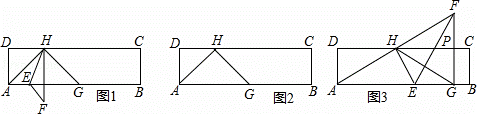
若一个正n边形的每个内角为156°，则这个正n边形的边数是（ ）
|
| A． | 13 | B． | 14 | C． | 15 | D． | 16 |
（r是⊙O的半径）．