题目内容
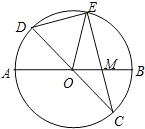 已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.
已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.(1)求证:AM•MB=EM•MC;
(2)连接DE,DE=
| 15 |
分析:(1)将乘积式化为比例式,然后证对应的三角形相似即可,即连接BE、AC,证△ACM∽△EBM;
(2)M是OB的中点,由此可求出AM、BM的长;Rt△DEC中,由勾股定理易求得EC的长,进而可用EM表示出MC,再将这些数据代入(1)的乘积式中,即可求出EM的长.
(2)M是OB的中点,由此可求出AM、BM的长;Rt△DEC中,由勾股定理易求得EC的长,进而可用EM表示出MC,再将这些数据代入(1)的乘积式中,即可求出EM的长.
解答: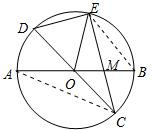 (1)证明:连接BE、AC.
(1)证明:连接BE、AC.
由圆周角定理,得:∠MEB=∠MAC,∠MBE=∠MCA
∴△MEB∽△MAC
∴
=
,即AM•MB=EM•MC;
(2)解:∵M是OB的中点,
∴OM=MB=2,AM=OA+OM=6
∵CD是⊙O的直径,
∴∠DEC=90°
Rt△DEC中,DE=
,CD=8
由勾股定理,得:CE=7
∴MC=CE-EM=7-EM
由(1)知:AM•MB=EM•MC,即:
(7-EM)×EM=6×2,解得EM=4(EM>MC)
所以EM的长为4.
 (1)证明:连接BE、AC.
(1)证明:连接BE、AC.由圆周角定理,得:∠MEB=∠MAC,∠MBE=∠MCA
∴△MEB∽△MAC
∴
| AM |
| EM |
| MC |
| MB |
(2)解:∵M是OB的中点,
∴OM=MB=2,AM=OA+OM=6
∵CD是⊙O的直径,
∴∠DEC=90°
Rt△DEC中,DE=
| 15 |
由勾股定理,得:CE=7
∴MC=CE-EM=7-EM
由(1)知:AM•MB=EM•MC,即:
(7-EM)×EM=6×2,解得EM=4(EM>MC)
所以EM的长为4.
点评:此题主要考查的是圆周角定理、勾股定理及相似三角形的判定和性质.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
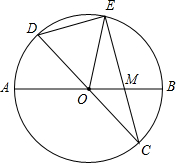 于点E,且EM>MC.连接DE,DE=
于点E,且EM>MC.连接DE,DE=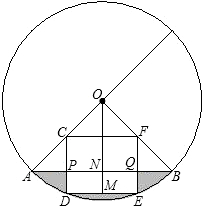 已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧
已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧
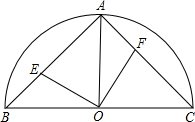 上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.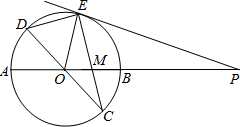 已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=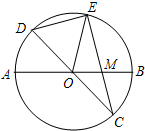 已知:如图,在半径为8的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为8的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=