题目内容
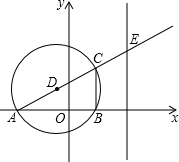 如图,以AC为直径的⊙D与x轴交于A、B两点,A、B的坐标分别为(-2,0)和(1,0),BC=
如图,以AC为直径的⊙D与x轴交于A、B两点,A、B的坐标分别为(-2,0)和(1,0),BC=| 3 |
(1)求以直线x=2为对称轴,且过C与原点O的抛物线的函数解析式,并判断此抛物线是否过点E,说明理由;
(2)设(1)中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值.
分析:(1)首先判断BC⊥AB,然后求出点C坐标,根据抛物线的对称轴为x=2,可设抛物线解析式是y=a(x-2)2+k,将(0,0)及点C的坐标代入可得出a、k的值,继而得出抛物线解析式,求出点E的坐标后,代入即可判断此抛物线是否过点E.
(2)根据题意画出图形,抛物线与x轴的另一个交点N(4,0),设M(x,y),过C,M分别作x轴的垂线,垂足为G,H,则根据S△CMN=SCGHM+S△HMN-S△CGN,可得△CMN的面积关于x、y的表达式,将y=-
(x-2)2+
,代入可得△CMN的面积关于x的表达式,利用配方法求最值即可.
(2)根据题意画出图形,抛物线与x轴的另一个交点N(4,0),设M(x,y),过C,M分别作x轴的垂线,垂足为G,H,则根据S△CMN=SCGHM+S△HMN-S△CGN,可得△CMN的面积关于x、y的表达式,将y=-
| ||
| 3 |
4
| ||
| 3 |
解答:解:(1)∵AC为⊙D的直径,
∴BC⊥AB,
∴由已知可得点C(1,
),
设抛物线解析式是y=a(x-2)2+k,
将(0,0)、(1,
)得:
,
解得:
,
故抛物线的解析式为:y=-
(x-2)2+
,
设直线x=2与x轴交于点F,则CB∥EF,
∴△ACB∽△AEF,
∴
=
,即
=
,
∴EF=
,
∴E(2,
),
当x=2时,y=-
(2-2)2+
=
,
∴抛物线经过点E.
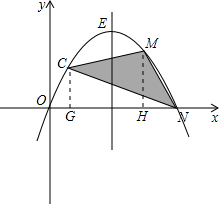
(2)抛物线与x轴的另一个交点N(4,0),设M(x,y),
过C,M分别作x轴的垂线,垂足为G,H,
S△CMN=SCGHM+S△HMN-S△CGN
=
(y+
)(x-1)+
y(4-x)-
×3×
=
+
x-2
=
[-
(x-2)2+
]+
x-2
=-
x2+
x-2
=-
(x-
)2+
(1≤x≤4),
当x=
时,S△CMN的最大值是
.
∴BC⊥AB,
∴由已知可得点C(1,
| 3 |
设抛物线解析式是y=a(x-2)2+k,
将(0,0)、(1,
| 3 |
|
解得:
|
故抛物线的解析式为:y=-
| ||
| 3 |
4
| ||
| 3 |
设直线x=2与x轴交于点F,则CB∥EF,
∴△ACB∽△AEF,
∴
| AB |
| AF |
| CB |
| EF |
| 3 |
| 4 |
| ||
| EF |
∴EF=
4
| ||
| 3 |
∴E(2,
4
| ||
| 3 |
当x=2时,y=-
| ||
| 3 |
4
| ||
| 3 |
4
| ||
| 3 |
∴抛物线经过点E.

(2)抛物线与x轴的另一个交点N(4,0),设M(x,y),
过C,M分别作x轴的垂线,垂足为G,H,
S△CMN=SCGHM+S△HMN-S△CGN
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
=
| 3y |
| 2 |
| ||
| 2 |
| 3 |
=
| 3 |
| 2 |
| ||
| 3 |
4
| ||
| 3 |
| ||
| 2 |
| 3 |
=-
| ||
| 2 |
5
| ||
| 2 |
| 3 |
=-
| ||
| 2 |
| 5 |
| 2 |
9
| ||
| 8 |
当x=
| 5 |
| 2 |
| 9 |
| 8 |
| 3 |
点评:本题考查了二次函数的综合,涉及了待定系数法求函数解析式、二次函数图象上点的坐标特征,难点在第二问,关键是作出图形,得出面积关于x的表达式,要求同学们熟练配方法求二次函数最值的应用.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 如图,以AB为直径的半圆O上有一点C,过A点作半圆的切线交BC的延长线于点D.
如图,以AB为直径的半圆O上有一点C,过A点作半圆的切线交BC的延长线于点D.
 如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD.
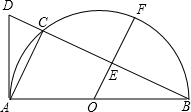
如图,以AB为直径的⊙O经过点P,C是⊙O上一点,连接PC交AB于点E,且∠ACP=60°,PA=PD. (2013•成都一模)如图,以AB为直径的⊙O是△ADC的外接圆,过点O作PO⊥AB,交AC于点E,PC的延长线交AB的延长线于点F,∠PEC=∠PCE.若△ADC是边长为1的等边三角形,则PC的长=
(2013•成都一模)如图,以AB为直径的⊙O是△ADC的外接圆,过点O作PO⊥AB,交AC于点E,PC的延长线交AB的延长线于点F,∠PEC=∠PCE.若△ADC是边长为1的等边三角形,则PC的长=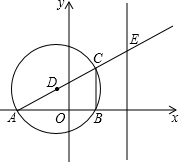 如图,以AC为直径的⊙D与x轴交于A、B两点,A、B的坐标分别为(-2,0)和(1,0),BC=
如图,以AC为直径的⊙D与x轴交于A、B两点,A、B的坐标分别为(-2,0)和(1,0),BC= .设直线AC与直线x=2交于点E.
.设直线AC与直线x=2交于点E.