题目内容
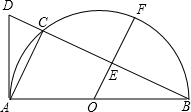如图，以AB为直径的半圆O上有一点C，过A点作半圆的切线交BC的延长线于点D．（1）求证：△ADC∽△BDA；
（2）过O点作AC的平行线OF分别交BC，
 |
| BC |
| 3 |
|
| AC |
分析：（1）根据切线的性质知：∠BAD=90°，由AB为半圆O的直径，可得：∠ACD=90°，再根据∠ADC=∠BDA，故：△ADC∽△BDA；
（2）作辅助线，连接OC，在Rt△OBE中，根据勾股定理可将半径求出，进而可将∠OBE和∠AOC的度数求出，代入弧长公式进行求解即可．
（2）作辅助线，连接OC，在Rt△OBE中，根据勾股定理可将半径求出，进而可将∠OBE和∠AOC的度数求出，代入弧长公式进行求解即可．
解答：（1）证明：∵AB为直径，
∴∠ACB=90°，
∴∠ACD=90°．
∵AD为半圆O的切线，
∴∠BAD=90°，
∴∠ACD=∠BAD．
又∵∠ADC=∠BDA，
∴△ADC∽△BDA．
（2）解：连接OC，
∵OE∥AC，
∴OE⊥BC，
∴BE=EC=
．
在Rt△OBE中，设OB=x，则有：x2=（
）2+（x-1）2
∴x=OB=2，
∴OE=1，
∴∠OBE=30°，
∴∠AOC=60°，
∴
的长=
=
．
∴∠ACB=90°，
∴∠ACD=90°．
∵AD为半圆O的切线，
∴∠BAD=90°，
∴∠ACD=∠BAD．
又∵∠ADC=∠BDA，
∴△ADC∽△BDA．
（2）解：连接OC，
∵OE∥AC，
∴OE⊥BC，
∴BE=EC=
| 3 |
在Rt△OBE中，设OB=x，则有：x2=（
| 3 |
∴x=OB=2，
∴OE=1，
∴∠OBE=30°，
∴∠AOC=60°，
∴
|
| AC |
| 60π×2 |
| 180 |
| 2π |
| 3 |
点评：本题主要考查相似三角形的判定及弧长的计算问题．
练习册系列答案
相关题目
10、如图，以AB为直径的半圆O上有两点D、E，ED与BA的延长线交于点C，且有DC=OE，若∠C=20°，则∠EOB的度数是（ ）
如图，以AB为直径的⊙O经过点P，C是⊙O上一点，连接PC交AB于点E，且∠ACP=60°，PA=PD．
（2013•成都一模）如图，以AB为直径的⊙O是△ADC的外接圆，过点O作PO⊥AB，交AC于点E，PC的延长线交AB的延长线于点F，∠PEC=∠PCE．若△ADC是边长为1的等边三角形，则PC的长=
如图，以AB为直径的⊙O与AD、DC、BC均相切，若AB=BC=4，则OD的长度为（ ）