题目内容
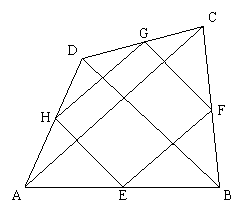
如图,已知∆ABC是等边三角形,边长为10,点D、E、F分别在边AB、BC、AC上,且AD=BE=CF,
(1)设AD为x,△ADF的面积为y,当x为何值时,△ADF的面积最大,最大面积是多少?
(2)当x为何值时,△ADF是直角三角形?

解:(1)因为AD为x,AD=BE=CF,所以AF=10-x……………1分
 过F作AB的垂线,垂足为H……………2分
过F作AB的垂线,垂足为H……………2分
因为∆ABC是等边三角形,所以∠A=60°,则FH=AF×sin60°=(10-x)× …………3分
…………3分
所以y= (10-x) ×
(10-x) × =-
=- +5x……………4分
+5x……………4分
所以x=-
 =
= =
= ……………5分
……………5分
y=- +5×
+5× =-
=- +
+ =
= ……………6分
……………6分
所以当x= ,△ADF的面积最大,最大面积是
,△ADF的面积最大,最大面积是 平方单位……………7分
平方单位……………7分
(2)如果△ADF是直角三角形,令∠ADF是直角根据勾股定理的逆定理得: +
+ =
=
则 +
+ =
=
解得: (舍去),
(舍去),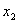 =
= ……………8分
……………8分
如果△ADF是直角三角形,令∠AFD是直角,根据勾股定理的逆定理得: +
+ =
=
则 +
+ =
= ,此方程无实数解
,此方程无实数解 ……………9分
……………9分
所以当x= 时,△ADF是直角三角形. ……………10分
时,△ADF是直角三角形. ……………10分

练习册系列答案
相关题目
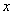 ,则下面所列方程正确的是( )
,则下面所列方程正确的是( ) B、
B、 C、
C、 D、
D、
 .7条
.7条 的正整数解是 .
的正整数解是 .