题目内容
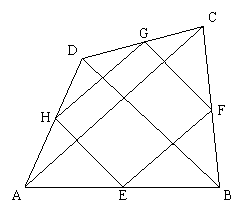
如图,在四边形ABCD中,对角线AC、BD互相垂直,点E、F、G、H分别是边AB、BC、CD、DA的中点,依次连结这四个中点得到四边形EFGH.
(1)求证:四边形EFGH是矩形;
(2)若AC=15,BD=10,求四边形EFGH的周长.
 |
解:(1)因为点E、F、G、H分别是边AB、BC、CD、DA的中点,
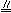
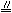
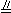
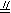 所以EF
所以EF  AC,GH
AC,GH  AC,因此,EF GH,同理EH FG
AC,因此,EF GH,同理EH FG
所以四边形EFGH是平行四边形. (4分)
又因为对角线AC、BD互相垂直,故EF与FG垂直.
所以四边形EFGH是矩形. (6分)
(2)因为EF= AC,FG=
AC,FG= BD,所以EF=7.5,FG=5
BD,所以EF=7.5,FG=5
于是,四边形EFGH的周长是2×(7.5+5)=25 (8分)

练习册系列答案
相关题目

 的扇形,.则这个圆锥底面半径是 .
的扇形,.则这个圆锥底面半径是 .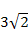 B. 4 C. 3 D.
B. 4 C. 3 D. 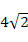
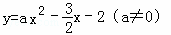 的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(10分)
的图象与x轴交于A、B两点,与y轴交于C点,已知B点坐标为(4,0).(10分)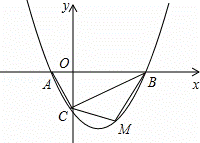
 烟花侧面包装纸的面积至少需要(解缝面积不计)( )
烟花侧面包装纸的面积至少需要(解缝面积不计)( ) rh B. 24rh+
rh B. 24rh+