题目内容
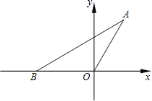
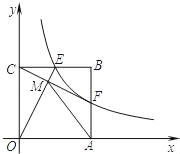
【题目】如图,点B的坐标是(4,4),作BA⊥x轴于点A,作BC⊥y轴于点C,反比例函数![]() (k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,OE与CF交于点M,连接AM.
(k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,OE与CF交于点M,连接AM.
(1)求反比例函数的函数解析式及点F的坐标;
(2)你认为线段OE与CF有何位置关系?请说明你的理由.
(3)求证:AM=AO.
【答案】(1)y=![]() ,点F的坐标是(4,2);(2)线段OE与CF的位置关系是OE⊥CF,理由见解析;(3)见解析.
,点F的坐标是(4,2);(2)线段OE与CF的位置关系是OE⊥CF,理由见解析;(3)见解析.
【解析】
(1)求出E的坐标,求出反比例函数的解析式,把x=4代入即可求出F的坐标;
(2)证△OCE≌△CBF,推出∠COE=∠BCF,求出∠ECF+∠CEO=90°即可;
(3)过M作MN⊥OC于N,证△CMO和△ECO相似,求出CM、OM,根据三角形的面积公式求出MN,根据勾股定理求出ON,得出M的坐标,根据勾股定理求出AM的值即可.
(1)解:∵正方形ABCO,B(4,4),E为BC中点,
∴OA=AB=BC=OC=4,CE=BE=2,F的横坐标是4,
∴E的坐标是(2,4),
把E的坐标代入y=![]() 得:k=8,
得:k=8,
∴y=![]() ,
,
∵F在双曲线上,
∴把F的横坐标是4代入得:y=2,
∴F(4,2),
答:反比例函数的函数解析式是y=![]() ,点F的坐标是(4,2).
,点F的坐标是(4,2).
(2)线段OE与CF的位置关系是OE⊥CF,
理由是:∵E的坐标是(2,4),点F的坐标是(4,2),
∴AF=4﹣2=2=CE,
∵正方形OABC,
∴OC=BC,∠B=∠BCO=90°,
∵在△OCE和△CBF中
 ,
,
∴△OCE≌△CBF,
∴∠COE=∠BCF,
∵∠BCO=90°,
∴∠COE+∠CEO=90°,
∴∠BCF+∠CEO=90°,
∴∠CME=180°﹣90°=90°,
即OE⊥CF.
(3)证明:∵OC=4,CE=2,由勾股定理得:OE=2![]() ,
,
过M作MN⊥OC于N,

∵OE⊥CF,
∴∠CMO=∠OCE=90°,
∵∠COE=∠COE,
∴△CMO∽△ECO,
∴![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() =
=![]() ,
,
解得:CM=![]() ,OM=
,OM=![]() ,
,
在△CMO中,由三角形的面积公式得:![]() ×OC×MN=
×OC×MN=![]() ×CM×OM,
×CM×OM,
即4MN=![]() ×
×![]() ,
,
解得:MN=![]() ,
,
在△OMN中,由勾股定理得:ON=![]() =
=![]() ,
,
即M(![]() ,
,![]() ),
),
∵A(4,0),
∴由勾股定理得:AM=4=AO,
即AM=AO.

 名校课堂系列答案
名校课堂系列答案【题目】小明平时喜欢玩“开心消消乐”游戏,本学期在学校组织的几次数学反馈性测试中,小明的数学成绩如下表:
月份 |
|
|
|
|
|
|
成绩(分) |
|
|
|
| ··· | ··· |
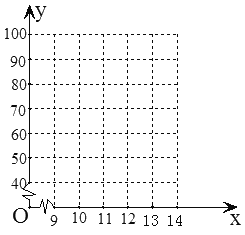
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在平面直角坐标系中描点;
(2)观察(1)中所描点的位置关系,猜想![]() 与
与![]() 之间的的函数关系,并求出所猜想的函数表达式;
之间的的函数关系,并求出所猜想的函数表达式;
(3)若小明继续沉溺于“开心消消乐“游戏,照这样的发展趋势,请你估计元月(此时![]() )份的考试中小明的数学成绩,并用一句话对小明提出一些建议.
)份的考试中小明的数学成绩,并用一句话对小明提出一些建议.