Question

如图所示，两个村子A、B在一条河CD的同侧，A、B两村到河边的距离分别为AC=1千米，BD=3千米，CD=3千米．现要在河边CD上建造一水厂，向A、B两村送水，铺设水管的工程费用为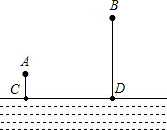每千米15000元，请你在CD上选择水厂位置，使铺设水管的费用最省，并求出最省的铺设水管的费用W．

Answer 1

分析：由于铺设水管的工程费用为每千米15000元，是一个定值，现在要在CD上选择水厂位置，使铺设水管的费用最省，意思是在CD上找一点P，使AP与BP的和最小，设M是A的对称点，使AP+BP最短就是使MP+BP最短．

解答：解：如图所示：延长AC到点M，使CM=AC；连接BM交CD于点P，
点P就是所选择的位置．（3分）
在直角三角形BMN中，
BN=3+1=4，MN=3，
∴MB=

MN2+BN2

=

32+42

=5（千米），
∴最短路线AP+BP=MB=5，
最省的铺设管道的费用为
W=5×15000=75000（元）
答：最省的铺设管道的费用是75000元．（10分）

点评：解这类问题的关键是将实际问题抽象或转化为几何模型，把两条线段的和转化为一条线段，运用三角形三边关系解决．