��Ŀ����
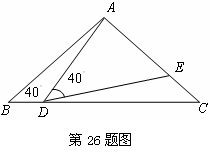
��ͼ���ڡ�ABC�У�AB=AC=2����B=40�㣬��D���߶�AB���˶���D����B��C�غϣ�������AD������ADE=40�㣬DE����AC����E.
��1������BDA=115��ʱ����BAD= ��, ��DEC= ���D��B��C�˶�ʱ����BDA�� �����С��������
��2����DC���ڶ���ʱ����ABD���DCEȫ�ȣ���˵�����ɣ�
��3�� �ڵ�D���˶������У���ADE����״�����ǵ����������������ԣ���ֱ��д����BDA�Ķ���.�������ԣ���˵������.
 |
�⣨1�� 25�㣻 115�㣻 С
��2����DC=2ʱ����ABD�ա�DCE���������£�
 �� DC=2��AB=2
�� DC=2��AB=2
�� DC=AB
�� AB=AC, ��B=40��
�� ��B=��C=40��
�� ��ADB=��DAC+��C
��DEC=��DAC+��ADE
 �ҡ�C=40�㣬��ADE=40��
�ҡ�C=40�㣬��ADE=40��
�� ��ADB=��DEC��
�ڡ�ABD���DCE��
�� ��B=��C
 ��ADB=��DEC
��ADB=��DEC
DC=AB
���ABD�ա�DCE��AAS��
��3������ͼ�������
�� ��BDA=110��
�� ��BDA=80��

��ϰ��ϵ�д�
 �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
�����Ŀ
 ������
������
 �ף�Ŀǰ����һ�����Ͳ���ֱ��Ϊ23150���ף��ÿ�ѧ��������ʾ�ò���ֱ���� �ף�����������Ч���֣���
�ף�Ŀǰ����һ�����Ͳ���ֱ��Ϊ23150���ף��ÿ�ѧ��������ʾ�ò���ֱ���� �ף�����������Ч���֣��� 
 ����
���� B.
B. C.
C. D.
D.
 B��
B�� C��
C�� D��
D��
 �ĵ����� ��
�ĵ����� ��