题目内容
10.在数轴上A点表示数-6,B点表示数8,这A,B两点正中的点表示的数字是1,A点和B点之间的距离是14;若点A表示的数为a,点B表示的数为b,(其中a<b),则A,B两点正中的点表示的数字是$\frac{a+b}{2}$,A点和B点之间的距离是b-a.分析 根据中点坐标公式,以及两点间距离公式即可求解.
解答 解:在数轴上A点表示数-6,B点表示数8,这A,B两点正中的点表示的数字是(-6+8)÷2=1,
A点和B点之间的距离是8-(-6)=14;
若点A表示的数为a,点B表示的数为b,(其中a<b),
则A,B两点正中的点表示的数字是 $\frac{a+b}{2}$,A点和B点之间的距离是b-a.
故答案为:1,14;$\frac{a+b}{2}$,b-a.
点评 本题考查数轴上两点间距离的求法:右边点的坐标减去左边点的坐标;或两点坐标差的绝对值.同时考查了中点坐标公式.

练习册系列答案
相关题目
5. 根据如图所示的流程图计算,若输入x的值为-1,则输出y的值为( )
根据如图所示的流程图计算,若输入x的值为-1,则输出y的值为( )
 根据如图所示的流程图计算,若输入x的值为-1,则输出y的值为( )
根据如图所示的流程图计算,若输入x的值为-1,则输出y的值为( )| A. | -2 | B. | -1 | C. | 7 | D. | 17 |
2.由表的对应值知,一元二次方程ax2+bx+c=0(a,b,c为常数,a≠0)的一个根的百分位上的数字是4.
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | -0.06 | -0.02 | 0.03 | 0.09 |
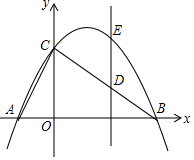 如图,Rt△ABC的三个顶点均落在平面直角坐标系的坐标轴上,OA=1,OB=4OA,∠ACB=90°,抛物线y=ax2+bx+c(a≠0)过A,B,C三点.
如图,Rt△ABC的三个顶点均落在平面直角坐标系的坐标轴上,OA=1,OB=4OA,∠ACB=90°,抛物线y=ax2+bx+c(a≠0)过A,B,C三点.