题目内容
 如图,直线y=
如图,直线y=| 1 |
| 2 |
| 1 |
| 2 |
考点:一次函数图象与几何变换
专题:计算题
分析:先确定A(-8,0)、B(0,4),过C作CD垂直y轴于D,如图,再证明△AOB≌△BDC,得到CD=OB=4,BD=OA=8,则OD=BD-OB=4,所以C((4,-4),然后利用待定系数法确定直线BC的解析式为y=-2x+4,则可确定它与x轴的交点坐标为(2,0),利用平行线的性质得到当AB向右平移,经过点(2,0)时,即AB向右移动10个单位时成直角三角形,此时
×2+m=0,解得m=-1.
| 1 |
| 2 |
解答: 解:直线y=
解:直线y=
x+4交x轴于点A,则A(-8,0),交y轴于点B,则B(0,4),
过C作CD垂直y轴于D,如图,
∵∠BAC=90°,
∴∠AOB=∠BCD,
在△AOB和△BDC中
,
∴△AOB≌△BDC,
∴CD=OB=4,BD=OA=8,
∴OD=BD-OB=4,
∴C((4,-4).
设直线BC的解析式为y=kx+b,把B(0,4)、C(4,-4)代入得
,解得
,则直线BC的解析式为y=-2x+4,它与x轴的交点坐标为(2,0),
∴当AB向右平移,经过点(2,0)时,即AB向右移动10个单位时成直角三角形,此时
×2+m=0,解得m=-1.
故答案为(4,-4),-1.
 解:直线y=
解:直线y=| 1 |
| 2 |
过C作CD垂直y轴于D,如图,
∵∠BAC=90°,
∴∠AOB=∠BCD,
在△AOB和△BDC中
|
∴△AOB≌△BDC,
∴CD=OB=4,BD=OA=8,
∴OD=BD-OB=4,
∴C((4,-4).
设直线BC的解析式为y=kx+b,把B(0,4)、C(4,-4)代入得
|
|
∴当AB向右平移,经过点(2,0)时,即AB向右移动10个单位时成直角三角形,此时
| 1 |
| 2 |
故答案为(4,-4),-1.
点评:本题考查了一次函数图象与几何变换:直线y=kx+b向下平移m(m>0)个单位的解析式为y=kx+b+m;直线y=kx+b向右平移n(n>0)个单位的解析式为y=k(x-n)+b.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
下列分解因式正确的是( )
| A、a2+6a+5=a(a+6)+5 |
| B、(a-b)2+4ab=(a+b)2 |
| C、(a+1)(a+2)=a2+3a+2 |
| D、a3b-ab=ab(a2-1) |
 如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=
如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=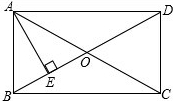 如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,且BE:ED=1:3.若BC=3,则AE的长为
如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,且BE:ED=1:3.若BC=3,则AE的长为 根据如图所示的计算程序,若x=1,则y=
根据如图所示的计算程序,若x=1,则y= 如图,△ABC的面积是
如图,△ABC的面积是