题目内容
12.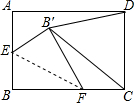 如图,在矩形ABCD中,AB=6,BC=8,点E为AB的中点,点F为BC边上任意一点,将△BEF沿EF翻折,点B的对应点为B′,则当△B′CD面积最小时折痕EF的长为3$\sqrt{2}$.
如图,在矩形ABCD中,AB=6,BC=8,点E为AB的中点,点F为BC边上任意一点,将△BEF沿EF翻折,点B的对应点为B′,则当△B′CD面积最小时折痕EF的长为3$\sqrt{2}$.
分析 当△B′CD面积最小时,B′到CD的距离最小,即B′到AB的距离最大,当B′到AB的距离=EB′时,此时B′到AB的距离最大,即EB′⊥AB,根据折叠的性质得到BE=B′E,∠B=∠EB′F=∠B′EB=90°,推出四边形EBFB′是正方形,得到EF=$\sqrt{2}$BE,于是得到距离.
解答 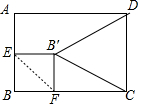 解:当△B′CD面积最小时,B′到CD的距离最小,即B′到AB的距离最大,
解:当△B′CD面积最小时,B′到CD的距离最小,即B′到AB的距离最大,
∴当B′到AB的距离=EB′时,此时B′到AB的距离最大,
即EB′⊥AB,
∵将△BEF沿EF翻折,点B的对应点为B′,
∴BE=B′E,∠B=∠EB′F=∠B′EB=90°,
∴四边形EBFB′是正方形,
∴EF=$\sqrt{2}$BE,
∵点E为AB的中点,
∴BE=3,
∴EF=3$\sqrt{2}$,
∴当△B′CD面积最小时折痕EF的长为3$\sqrt{2}$,
故答案为:3$\sqrt{2}$.
点评 本题考查了翻折变换-折叠问题,矩形的性质,正方形的判定和性质,正确的作出图形是解题的关键.

练习册系列答案
相关题目
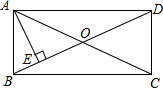 如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$.
如图,矩形ABCD的对角线AC,BD交于点O,AE⊥BD于点E,且∠DAE:∠BAE=2:1,AE=$\sqrt{3}$,则矩形ABCD的面积是4$\sqrt{3}$. 如图,AB是⊙O的直径,AB=4$\sqrt{3}$,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
如图,AB是⊙O的直径,AB=4$\sqrt{3}$,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.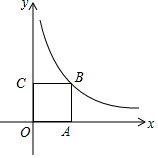 如图,点B在反比例函数y=$\frac{4}{x}$(x>0)的图象上,点A,C分别在x轴、y轴正半轴上,且四边形OABC为正方形.
如图,点B在反比例函数y=$\frac{4}{x}$(x>0)的图象上,点A,C分别在x轴、y轴正半轴上,且四边形OABC为正方形.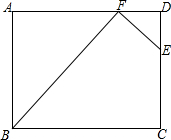 如图,ABCD是长方形,AB=6,BC=8,CE=4,四边形BCEF的面积是30,那么三角形DEF的面积是多少?
如图,ABCD是长方形,AB=6,BC=8,CE=4,四边形BCEF的面积是30,那么三角形DEF的面积是多少?