题目内容
 已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC,连接DE,DE=
已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC,连接DE,DE= .
.
(1)求证:AM•MB=EM•MC;
(2)求EM的长.
证明:(1)∵AB、CE是⊙O内的两条相交弦,
∴AM•MB=EM•MC;
(2)∵M是OB中点,圆半径R=4,
∴OM=MB=2,
∴AM=6,
∵CD是直径,
∴∠CED=90°,
∴CE2=CD2-DE2,
∴CE= =7,
=7,
设EM=x,6×2=x•(7-x),
解得x=3或x=4,
∵EM>MC,
∴EM=4.
分析:(1)直接根据相交弦定理可得AM•MB=EM•MC;
(2)根据M是OB中点,再结合⊙O半径等于4,易求BM、AM,而CD是直径,于是∠CED=90°,根据勾股定理易求CE,再结合(1)中AM•MB=EM•MC,设EM=x,易得6×2=x•(7-x),解关于x的方程可得x=3或4,而EM>MC,从而可求EM=4.
点评:本题考查了相交弦定理、勾股定理、解一元二方程,解题的关键是注意先求出BM,以及CE.

∴AM•MB=EM•MC;
(2)∵M是OB中点,圆半径R=4,
∴OM=MB=2,
∴AM=6,
∵CD是直径,
∴∠CED=90°,
∴CE2=CD2-DE2,
∴CE=
 =7,
=7,设EM=x,6×2=x•(7-x),
解得x=3或x=4,
∵EM>MC,
∴EM=4.
分析:(1)直接根据相交弦定理可得AM•MB=EM•MC;
(2)根据M是OB中点,再结合⊙O半径等于4,易求BM、AM,而CD是直径,于是∠CED=90°,根据勾股定理易求CE,再结合(1)中AM•MB=EM•MC,设EM=x,易得6×2=x•(7-x),解关于x的方程可得x=3或4,而EM>MC,从而可求EM=4.
点评:本题考查了相交弦定理、勾股定理、解一元二方程,解题的关键是注意先求出BM,以及CE.

练习册系列答案
相关题目
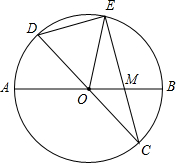 于点E,且EM>MC.连接DE,DE=
于点E,且EM>MC.连接DE,DE=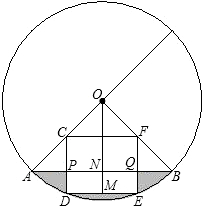 已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧
已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧
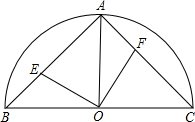 上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.
上滑动并保持AE=CF,但点F不与A、C重合,点E不与A、B重合.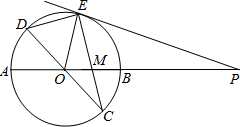 已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=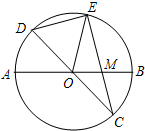 已知:如图,在半径为8的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=
已知:如图,在半径为8的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连接DE,DE=