Question

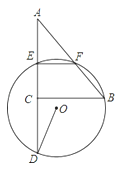
【题目】如图，△ABC中，AC=3，BC=4，∠ACB=90°，E、F分别为AC、AB的中点，过E、F两点作⊙O，延长AC交⊙O于D．若∠CDO=∠B，则⊙O的半径为（　　）

A. 4 B. 2 C. D.

Answer 1

【答案】C

【解析】解：连接OF交BC于G，连接OE，∵E、F分别为AC、AB的中点，∴EF∥BC，EF=BC=2，EC=AC=．∵OE=OF，∴∠OEF=∠OFE．∵EF∥BC，∴∠DEF=∠DCB=90°，∴DF为直径，∴∠BGF=∠OFE．∵∠D=∠EOF，∠CDO=∠B，∴∠EOF=∠B，∴∠OEF=∠BFG，∴∠BGF=∠BFG，∴BG=BF=，CG=．∵EF∥BC，∴CD：DE=CG：EF，∴CD=3CE=．在Rt△DFE中，EF=2，DE=6，DF=，OD=．故选C．