题目内容
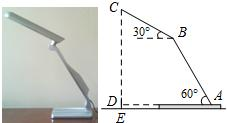
如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据: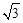 ≈1.732)
≈1.732)
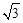 ≈1.732)
≈1.732)
51.6.
试题分析:要求CE就要考虑直角三角形,所以作辅助线:过点B作BF⊥CD于F,作BG⊥AD于G. 得到两个直角三角形和一个矩形. 这样利用解直角三角形就易求出.
试题解析:如图,过点B作BF⊥CD于F,作BG⊥AD于G..
在Rt△BCF中,∠CBF=30°,∴CF=BC·sin30°=30×
 =15.
=15.在Rt△ABG中,∠BAG=60°,∴BG=AB·sin60°=40×
 =20
=20 .
.∴CE=CF+FD+DE=15+20
 +2=17+20
+2=17+20 ≈51.64≈51.6(cm).
≈51.64≈51.6(cm).答:此时灯罩顶端C到桌面的高度CE约是51.6cm.


练习册系列答案
相关题目
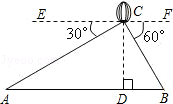
 △
△ 中,
中, ,
, ,
, .
.
 的长;(2)求
的长;(2)求 的值.
的值.


 如图那样折叠,使点
如图那样折叠,使点 与点
与点 重合,折痕为
重合,折痕为 ,则
,则 的值是________
的值是________
 ,则锐角A的度数是 ( )
,则锐角A的度数是 ( ) 的正切值是
的正切值是 ,则
,则 的值是【 】
的值是【 】




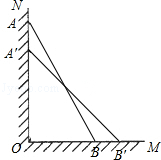
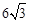 米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.
米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.