题目内容
如图,一根长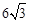 米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.
米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.
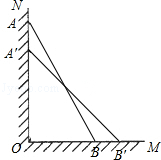
(1)求OB的长;
(2)当AA′=1米时,求BB′的长.
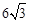 米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.
米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.
(1)求OB的长;
(2)当AA′=1米时,求BB′的长.
解:(1)根据题意可知:AB=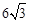 ,∠ABO=60°,∠AOB=90°,
,∠ABO=60°,∠AOB=90°,
在Rt△AOB中,∵cos∠ABO= ,∴OB=ABcos∠ABO=
,∴OB=ABcos∠ABO=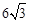 cos60°=
cos60°= (米)。
(米)。
∴OB的长为 米。
米。
(2)根据题意可知A′B′=AB=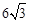 米,
米,
在Rt△AOB中,∵sin∠ABO= ,∴OA=ABsin∠ABO=
,∴OA=ABsin∠ABO=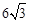 sin60°=9(米)。
sin60°=9(米)。
∵OA′=OA﹣AA′,AA′=1米,∴OA′=8米。
在Rt△A′OB′中,根据勾股定理,训OB′= 米,
米,
∴BB′=OB′﹣OB=( ﹣
﹣ )米。
)米。
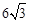 ,∠ABO=60°,∠AOB=90°,
,∠ABO=60°,∠AOB=90°,在Rt△AOB中,∵cos∠ABO=
 ,∴OB=ABcos∠ABO=
,∴OB=ABcos∠ABO=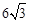 cos60°=
cos60°= (米)。
(米)。∴OB的长为
 米。
米。(2)根据题意可知A′B′=AB=
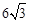 米,
米,在Rt△AOB中,∵sin∠ABO=
 ,∴OA=ABsin∠ABO=
,∴OA=ABsin∠ABO=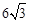 sin60°=9(米)。
sin60°=9(米)。∵OA′=OA﹣AA′,AA′=1米,∴OA′=8米。
在Rt△A′OB′中,根据勾股定理,训OB′=
 米,
米,∴BB′=OB′﹣OB=(
 ﹣
﹣ )米。
)米。试题分析:(1)由已知数据解直角三角形AOB即可;
(2)首先求出OA的长和OA′的长,再根据勾股定理求出OB′的长即可。

练习册系列答案
相关题目
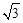 ≈1.732)
≈1.732)




 ≈1.41,
≈1.41, ≈1.73)
≈1.73)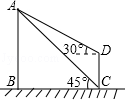
 ,(说明:本题不能使用计算器)
,(说明:本题不能使用计算器) .
. km的C处.
km的C处.
 .
.