题目内容
16.已知a是方程x2-2006x+1=0的一个根,试求代数式a2-2005a+$\frac{2006}{{a}^{2}+1}$的值.分析 先把x=a代入方程,可得a2-2006a+1=0,进而可得a2-2006a=-1,a2+1=2006a,进而可求a2-2005a=a-1,然后把a2-2005a与a2+1的值整体代入所求代数式求值即可.
解答 解:∵把x=a代入方程,可得a2-2006a+1=0,
∴a2-2006a=-1,a2+1=2006a,
∴a2-2005a=a-1,
∴a2-2005a+$\frac{2006}{{a}^{2}+1}$=a-1+$\frac{1}{a}$=$\frac{{a}^{2}-a+1}{a}$=$\frac{2005a}{a}$=2005.
点评 本题考查了一元二次方程的解,解题的关键是注意解与方程的关系,以及整体代入.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列说法中正确的是( )
| A. | 最小的整数是0 | |
| B. | 互为相反数的两个数的绝对值相等 | |
| C. | 有理数分为正有理数和负有理数 | |
| D. | 如果两个数的绝对值相等,那么这两个数相等 |
4.如果a+b=0,那么实数a、b的值是( )
| A. | 互为相反数 | B. | 互为倒数 | C. | 都是0 | D. | 至少有一个0 |
1.在下列长度的四组线段中,能组成三角形的是( )
| A. | 3,7,15 | B. | 1,2,4 | C. | 5,5,10 | D. | 2,3,3 |
6.点M(-5,2)关于x轴对称的坐标是( )
| A. | (-5,-2) | B. | (5,-2) | C. | (5,2) | D. | (-5,2) |
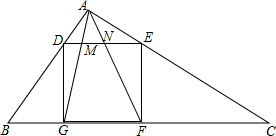 如图,在Rt△ABC中,∠BAC=90°,四边形DEFG为内接于△ABC的正方形,AG、AF交DE于点M、N,若$\frac{AB}{AC}$=$\frac{{x}^{2}}{{y}^{2}}$,求DM:MN:NE.
如图,在Rt△ABC中,∠BAC=90°,四边形DEFG为内接于△ABC的正方形,AG、AF交DE于点M、N,若$\frac{AB}{AC}$=$\frac{{x}^{2}}{{y}^{2}}$,求DM:MN:NE.