题目内容
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
(1)求证: ;
;
(2)判断AF与BD是否平行,并说明理由.
 |
1)由折叠可知:∠CDB =∠EDB
∵四边形ABCD是平行四边形
∴DC∥AB
∴∠CDB =∠EBD
∴∠EDB=∠EBD
(2) ∵∠EDB=∠EBD
∴DE=BE
由折叠可知:DC=DF
∵四边形ABCD是平行四边形
∴DC=AB
∴AE=EF
∴∠EAF=∠EFA
△BED中, ∠EDB+∠EBD+∠DEB=180°
即2∠EDB+∠DEB=180°
同理△AEF中,2∠EFA+∠AEF=180°
∵∠DEB=∠AEF
∴∠EDB= ∠EFA
∴AF∥BD

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 0 000元,将220 000 000 000用科学记数法表示为____________.
0 000元,将220 000 000 000用科学记数法表示为____________. .
. 在实数范围内有意义,则
在实数范围内有意义,则 的取值范围是 .
的取值范围是 . .
.  ,且与抛物线
,且与抛物线 交于A,B两点,其中点A的横坐标是
交于A,B两点,其中点A的横坐标是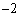 .
. 在点C,使得△ABC是直角三角形?若存在,求出点C的坐标;若不存在,请说明理由;
在点C,使得△ABC是直角三角形?若存在,求出点C的坐标;若不存在,请说明理由; ,当点M的横坐标为何值时,
,当点M的横坐标为何值时,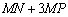 的长度最大?最大值是多少?
的长度最大?最大值是多少?
 (
( )与
)与 在同一坐标系中的大致图像是( )
在同一坐标系中的大致图像是( )
 中,点
中,点 、
、 、
、 、
、 分别在边
分别在边 、
、 、
、 、
、 上,
上, ,
, ,且
,且 平分
平分 .
. ≌
≌ ;
; 是菱形.
是菱形. 
