题目内容
8.一列数:a1,a2,a3,…an,…,其中a1=$\frac{4}{3}$,a2=$\frac{13}{9}$,且当n≥3时,an-an-1=$\frac{1}{3}$(an-1-an-2),用含n的式子表示an的结果是$\frac{3}{2}$-$\frac{1}{2×{3}^{n}}$.分析 根据an-an-1=$\frac{1}{3}$(an-1-an-2),依次写出相邻两项之差,再左右两边同时累加得出an-a1=$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$,令$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$=A,A-$\frac{1}{3}$A得出A的值,将其代入an-a1中,表示出an即可.
解答 解:∵an-an-1=$\frac{1}{3}$(an-1-an-2),
∴有an-an-1=$\frac{1}{3}({a}_{n-1}-{a}_{n-2})$=($\frac{1}{3}$)n-2(a2-a1),an-1-an-2=$\frac{1}{3}({a}_{n-2}-{a}_{n-3})$=($\frac{1}{3}$)n-3(a2-a1),…,a3-a2=$\frac{1}{3}({a}_{2}-{a}_{1})$,a2-a1=$\frac{1}{9}$=$(\frac{1}{3})^{2}$,
左右两边同时累加得an-a1=$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$,
令$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$=A,则$\frac{1}{3}$A=$\frac{1}{{3}^{3}}$+$\frac{1}{{3}^{4}}$…+$\frac{1}{{3}^{n+1}}$,
A-$\frac{1}{3}$A=$\frac{1}{{3}^{2}}$-$\frac{1}{{3}^{n+1}}$,解得:A=$\frac{1}{6}$-$\frac{1}{2×{3}^{n}}$.
∴an=A+a1=$\frac{1}{6}$-$\frac{1}{2×{3}^{n}}$+$\frac{4}{3}$=$\frac{3}{2}$-$\frac{1}{2×{3}^{n}}$.
故答案为:$\frac{3}{2}$-$\frac{1}{2×{3}^{n}}$.
点评 本题考查了规律型中得数字的变化类,解题的关键是找出an-a1=$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$.本题属于中档题,难度不大,因为初中没有学过等比数列的求和公式,故此处用错位相减法来推导出结论.

 a,b在数轴上的位置如图,化简|a+b|的结果是( )
a,b在数轴上的位置如图,化简|a+b|的结果是( )| A. | -a-b | B. | a+b | C. | a-b | D. | b-a |
| A. | 1和2之间 | B. | 2和3之间 | C. | 3和4之间 | D. | 4和5之间 |
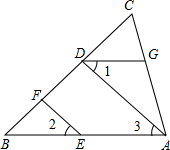 如图,EF∥AD,∠1=∠2,猜想∠BAC与∠DGA的关系,并说明理由.
如图,EF∥AD,∠1=∠2,猜想∠BAC与∠DGA的关系,并说明理由.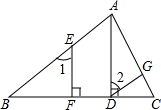 已知:如图,DG∥AB,AD⊥BC于D,EF⊥BC于F,求证:∠1=∠2.
已知:如图,DG∥AB,AD⊥BC于D,EF⊥BC于F,求证:∠1=∠2. 正方形ABCD中,点E为AB的中点,若将△BCE沿CE对折,点B将落在点F处,连接EF并延长交AD、CD的延长线分别于G、H.
正方形ABCD中,点E为AB的中点,若将△BCE沿CE对折,点B将落在点F处,连接EF并延长交AD、CD的延长线分别于G、H. 如图,正方形ACEF的边长为2,以AC为一边在同侧做等腰三角形ABC,且∠BAC=150°,BC交AE于点D,下列结论:①EF=ED;②S△DEC=1+$\frac{\sqrt{3}}{3}$;③AD+CD=BD,④S△ABD=$\frac{\sqrt{3}}{3}$,其中正确结论的序号是②③④.
如图,正方形ACEF的边长为2,以AC为一边在同侧做等腰三角形ABC,且∠BAC=150°,BC交AE于点D,下列结论:①EF=ED;②S△DEC=1+$\frac{\sqrt{3}}{3}$;③AD+CD=BD,④S△ABD=$\frac{\sqrt{3}}{3}$,其中正确结论的序号是②③④.