题目内容
一个三角形的两边长为3和6，第三边的边长是（x-3）（x-4）=0的根，则这个三角形的周长是（ ）
| A、13 | B、12 |
| C、11和13 | D、12或13 |
考点：解一元二次方程-因式分解法,三角形三边关系
专题：
分析：先解方程，求出x的值，再根据三角形三边关系舍去不合题意的解，再根据周长公式求解即可．
解答：解：∵（x-2）（x-4）=0，
∴x1=3，x2=4，
当x=3时，3+3=6（不合题意，舍去），
∴x=4，
∴这个三角形的周长=3+4+6=13．
故选A．
∴x1=3，x2=4，
当x=3时，3+3=6（不合题意，舍去），
∴x=4，
∴这个三角形的周长=3+4+6=13．
故选A．
点评：本题考查了因式分解法解一元二次方程以及三角形三边关系，此题比较简单，易于掌握．
练习册系列答案
相关题目
为了绿化校园，我校决定修建一块长方形草坪，长30米，宽20米，并在草坪上修建如图所示的十字路，设小路的宽为x米．平面直角坐标系内，若点A（3，-2）与点B（a，b）关于y轴对称，则下列结论中正确的是（ ）
| A、a=3，b=-2 |
| B、a=3，b=2 |
| C、a=-3，b=2 |
| D、a=-3，b=-2 |
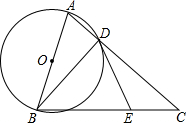如图，在△ABC中，AC=BC，以AB为直径的⊙O交AC边于点D，点E在BC上，连结BD，DE，∠CDE=∠ABD．