题目内容
 如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:
如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:(1)∠EDC的度数;
(2)若∠BCD=n°,试求∠BED的度数.(用含n的式子表示)
考点:平行线的性质
专题:
分析:(1)根据平行线的性质可得∠BAD=∠ADC=80°,再根据角平分线的性质可得∠EDC=
∠ADC;
(2)首先根据三角形内角和的性质可得∠1=180°-40°-n°=140°-n°,进而得到∠2的度数,然后再根据内角和定理可得∠BED的度数.
| 1 |
| 2 |
(2)首先根据三角形内角和的性质可得∠1=180°-40°-n°=140°-n°,进而得到∠2的度数,然后再根据内角和定理可得∠BED的度数.
解答:解:(1)∵AB∥CD,
∴∠BAD=∠ADC=80°,
∵DE平分∠ADC,
∴∠EDC=
∠ADC=
×80°=40°;
(2)∵∠BCD=n°,∠EDC=40°,
∴∠1=180°-40°-n°=140°-n°,
∴∠2=140°-n°,
∵AB∥CD,
∴∠ABC=∠BCD=n°,
∵BE平分∠ABC,
∴∠EBC=
n°,
∴∠E=180°-
n°-(140°-n°)=40°+
n°.
∴∠BAD=∠ADC=80°,
∵DE平分∠ADC,
∴∠EDC=
| 1 |
| 2 |
| 1 |
| 2 |

(2)∵∠BCD=n°,∠EDC=40°,
∴∠1=180°-40°-n°=140°-n°,
∴∠2=140°-n°,
∵AB∥CD,
∴∠ABC=∠BCD=n°,
∵BE平分∠ABC,
∴∠EBC=
| 1 |
| 2 |
∴∠E=180°-
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了平行线的性质,以及角平分线的性质,关键是掌握两直线平行内错角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )
小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )A、600-250
| ||
B、600
| ||
C、350+350
| ||
D、500
|
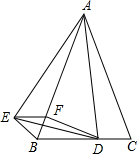 如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.
如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF.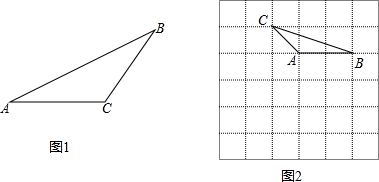
 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.