题目内容
在等腰Rt△ABC中,AB=BC点E在BC上,以AE为边作正方形AEMN,EM交AB于F,连结BM.(1)求证:BM⊥AB
(2)若CE=2BE,求
 的值.
的值. |
(1)连结AM,证△ACE~△ABM可得∠ABM=∠ACE=90°.
(2)过M作GM//BC交AB于G,由△ACE~△ABM得BM= CE
CE
设BE=1,则CE=2,BM= ,在Rt△BGM中,MG=
,在Rt△BGM中,MG= BM=4
BM=4
由BC//MG得 ∴AE="EM=5EF " ∴
∴AE="EM=5EF " ∴ =5解析:
=5解析:
略
(2)过M作GM//BC交AB于G,由△ACE~△ABM得BM=
 CE
CE设BE=1,则CE=2,BM=
 ,在Rt△BGM中,MG=
,在Rt△BGM中,MG= BM=4
BM=4由BC//MG得
 ∴AE="EM=5EF " ∴
∴AE="EM=5EF " ∴ =5解析:
=5解析:略

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 19、如图在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于D,若AB=10,则△BDE的周长等于
19、如图在等腰Rt△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于D,DE⊥AB于D,若AB=10,则△BDE的周长等于 16、如图,在等腰Rt△ABC中,∠A=90°,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接OP将线段OP绕O逆时针旋转90°得到线段OD,要使点D恰好落在BC上,则AP的长度等于
16、如图,在等腰Rt△ABC中,∠A=90°,AC=9,点O在AC上,且AO=2,点P是AB上一动点,连接OP将线段OP绕O逆时针旋转90°得到线段OD,要使点D恰好落在BC上,则AP的长度等于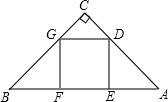 点G在边BC上.
点G在边BC上. (2013•怀化)如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(2013•怀化)如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.