题目内容
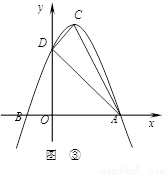
已知,如图,已知AD、AE分别是△ABC的中线,高线,且AB=5cm,AC=3cm;则△ABD和△ADC的周长之差等于 cm;△ABD与△ACD的面积关系是 .

【答案】
2,相等
【解析】
试题分析:根据△ABD的周长=AB+AD+BD,△ACD的周长=AC+AD+CD,AD是BC的中线,可得△ABD与△ACD的周长的差=AB-AC,三角形的中线把三角形分成面积相等的两个三角形,据此答题即可.
△ABD的周长=AB+AD+BD,△ACD的周长=AC+AD+CD,
∵AD是BC的中线,
∴BD=CD,
∵AB=5cm,AC=3cm,
∴△ABD的周长-△ACD的周长=AB+AD+BD-AC-AD-CD=AB-AC=2(cm),
∵△ABD与△ACD的底相等,高都是AE,
∴它们的面积相等.
考点:本题考查了三角形的中线概念和性质
点评:解答本题的关键是熟练掌握三角形的中线把三角形分成面积相等的两个三角形.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
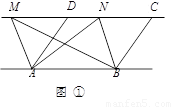
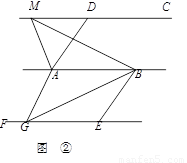
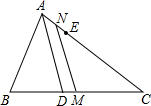 如图,已知AD为△ABC的角平分线,AB<AC,在AC上截取CE=AB,M、N分别为BC、AE的中点.求证:MN∥AD.
如图,已知AD为△ABC的角平分线,AB<AC,在AC上截取CE=AB,M、N分别为BC、AE的中点.求证:MN∥AD.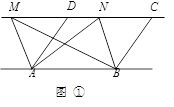
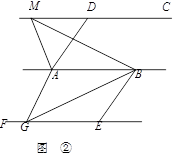
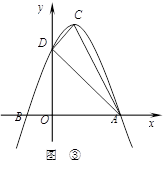
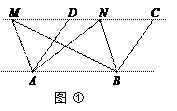

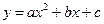 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
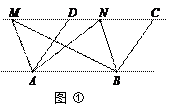
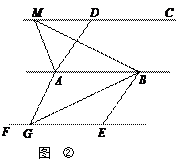
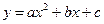 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
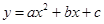 的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线
的顶点为C(1,4),交x轴于点A(3,0),交y轴于点D.试探究在抛物线