题目内容
把一个自然数所有数位上的数字先平方再求和得到一个新数,叫做第一次运算,再把所得新数所有数位上的数字先平方再求和又将得到一个新数,叫做第二次运算,……如此重复下去,若最终结果为1,我们把具有这种特征的自然数称为“快乐数”.例如:
 ,
,
 ,
,
所以32和70都是“快乐数”.
(1)写出最小的两位“快乐数”;判断19是不是“快乐数”;请证明任意一个“快乐数”经过若干次运算后都不可能得到4;
(2)若一个三位“快乐数”经过两次运算后结果为1,把这个三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2,求出这个“快乐数” .
解:(1)最小的两位“快乐数”10, ……………………1分
19是快乐数. ……………………2分
证明:由题意只需证明数字4经过若干次运算后都不会出现数字1.因为

37出现两次,所以后面将重复出现,永远不会出现1,所以任意一个“快乐数”经过若干次运算后都不可能得到4. ……………………5分
(2)设三位“快乐数”为 ,由题意,经过两次运算后结果为1,所以第一次运算后结果一定是10或者100,所以
,由题意,经过两次运算后结果为1,所以第一次运算后结果一定是10或者100,所以 ,又因为
,又因为
 ,所以当
,所以当 时,因为
时,因为
(1)当 ,
, ,
, 三位“快乐数”为130,103
三位“快乐数”为130,103
(2)当 ,
, ,
,
(3)当 ,
, ,
, 三位“快乐数”为310,301
三位“快乐数”为310,301
同理当 时,因为
时,因为 , 所以三位“快乐数”有680,608,806,860.综上一共有130,103,310,301,680,608,806,860八个. ……………………8分
, 所以三位“快乐数”有680,608,806,860.综上一共有130,103,310,301,680,608,806,860八个. ……………………8分
又因为三位“快乐数”与它的各位上的数字相加所得的和被8除余数是2,所以只有310和860满足已知条件. ……………………10分

 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案为了掌握某次数学模拟考试卷的命题质量与难度系数,命题教师选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组:第一组75~90;第二组90~105;第三组105~120;第四组120~135;第五组135~150.统计后得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:
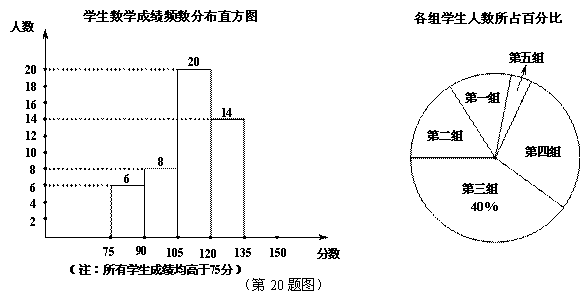 |
请将频数分布直方图补充完整;若老师找到第五组中一个学生的语文、数学、英语三科成绩,如下表.老师将语文、数学、英语成绩按照3:5:2的比例给出这位同学的综合分数.求此同学的综合分数.
| 科目 | 语文 | 数学 | 英语 |
| 得分 | 120 | 146 | 140 |


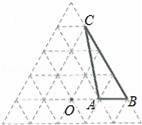

 中,AB=2
中,AB=2 , AD=6,cot∠ABC=
, AD=6,cot∠ABC= ,将边AB绕点A旋转,使得点B 落在平行四边形 ABCD的边上,其对应点为B'(点B'不与点B 重合),那么sin∠CAB'__________.
,将边AB绕点A旋转,使得点B 落在平行四边形 ABCD的边上,其对应点为B'(点B'不与点B 重合),那么sin∠CAB'__________.
 的图像经过点A(3,y1)和点B(5,y2),且y1>y2,则m的取值范围是 .
的图像经过点A(3,y1)和点B(5,y2),且y1>y2,则m的取值范围是 . (ab≠0),那么下列比例式变形正确的是( )
(ab≠0),那么下列比例式变形正确的是( ) B.
B. C.
C. D.
D.
 ,其中 x 满足 x2+x-2=0.
,其中 x 满足 x2+x-2=0.