题目内容
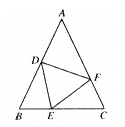
【题目】如图,ΔABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是( )
A.75°B.70°C.65°D.60°
【答案】C
【解析】
首先证明△DBE≌△ECF,进而得到∠EFC=∠DEB,再根据三角形内角和计算出∠CFE+∠FEC的度数,进而得到∠DEB+∠FEC的度数,然后可算出∠DEF的度数.
解:∵AB=AC,
∴∠B=∠C,
在△DBE和△ECF中,
 ,
,
∴△DBE≌△ECF(SAS),
∴∠EFC=∠DEB,
∵∠A=50°,
∴∠C=(180°-50°)÷2=65°,
∴∠CFE+∠FEC=180°-65°=115°,
∴∠DEB+∠FEC=115°,
∴∠DEF=180°-115°=65°,
故选:C.

练习册系列答案
相关题目