题目内容
如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.
(1)求证:△ADP≌△ECP;
(2)若BP=n•PK,试求出n的值;
(3)作BM丄AE于点M,作KN丄AE于点N,连结MO、NO,如图2所示,请证明△MON是等腰三角形,并直接写出∠MON的度数.
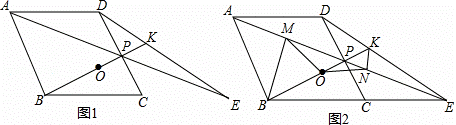
(1)证明:∵四边形ABCD为菱形,
∴AD∥BC,
∴∠DAP=∠CEP,∠ADP=∠ECP,
在△ADP和△ECP中,
 ,
,
∴△ADP≌△ECP;
(2)如图1,作PI∥CE交DE于I,
则 =
= ,又点P是CD的中点,
,又点P是CD的中点,
∴ =
= ,
,
∵△ADP≌△ECP,
∴AD=CE,
∴ =
= =
= ,
,
∴BP=3PK,
∴n=3;
(3)如图2,作OG⊥AE于G,
∵BM丄AE于,KN丄AE,
∴BM∥OG∥KN,
∵点O是线段BK的中点,
∴MG=NG,又OG⊥MN,
∴OM=ON,
即△MON是等腰三角形,
由题意得,△BPC,△AMB,△ABP为直角三角形,
设BC=2,则CP=1,由勾股定理得,BP= ,
,
则AP= ,
,
根据三角形面积公式,BM= ,
,
由(2)得,PB=3PO,
∴OG= BM=
BM= ,
,
MG= MP=
MP= ,
,
tan∠MOG= =
= ,
,
∴∠MOG=60°,
∴∠MON的度数为120°.



练习册系列答案
相关题目
某教研机构为了了解初中生课外阅读名著的现状,随机抽取了某校50名初中生进行调查,依据相关数据绘制成了以下不完整的统计图,请根据图中信息解答下列问题:
| 类别 | 重视 | 一般 | 不重视 |
| 人数 | a | 15 | b |
(1)求表格中a,b的值;
(2)请补全统计图;
(3)若某校共有初中生2000名,请估计该校“重视课外阅读名著”的初中生人数.

 )÷
)÷ ,其中a=
,其中a= +1.
+1.
 ﹣12×2﹣2;
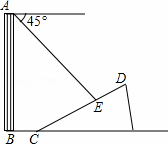
﹣12×2﹣2; ,山坡坡面上点 E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
,山坡坡面上点 E处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.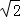 ≈1.414,
≈1.414,