题目内容
在等腰三角形ABC中，已知两条边分别是3和7，则△ABC的周长等于________．
17
分析：从当等腰三角形的腰长为7，底边长为3时，当等腰三角形的腰长为3，底边长为7时，两种情况去分析即可．
解答：当等腰三角形的腰长为7，底边长为3时，
因为7+3＞7，所以可构成三角形，其周长为7+3+7=17；
当等腰三角形的腰长为3，底边长为7时，
因为3+3＜7，所以不能构成三角形．
故答案为：17．
点评：此题主要考查学生对等腰三角形的性质和三角形三边关系的理解和掌握，尽管当等腰三角形的腰长为3，底边长为7时，不能构成三角形，但仍要采用分类讨论的思想，这也是学生容易忽视的地方．
分析：从当等腰三角形的腰长为7，底边长为3时，当等腰三角形的腰长为3，底边长为7时，两种情况去分析即可．
解答：当等腰三角形的腰长为7，底边长为3时，
因为7+3＞7，所以可构成三角形，其周长为7+3+7=17；
当等腰三角形的腰长为3，底边长为7时，
因为3+3＜7，所以不能构成三角形．
故答案为：17．
点评：此题主要考查学生对等腰三角形的性质和三角形三边关系的理解和掌握，尽管当等腰三角形的腰长为3，底边长为7时，不能构成三角形，但仍要采用分类讨论的思想，这也是学生容易忽视的地方．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
如图：在等腰三角形ABC中，AB=AC，∠A=40°，则∠B=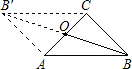
在等腰三角形ABC中，∠C=90°，BC=2cm．如果以AC的中点O为旋转中心，将这个三角形旋转180°，点B落在点B′处，那么点B′与点B的原来位置相距
如图所示，在等腰三角形ABC中，AB=AC=13cm，底边BC=10cm，求底边上的高AD和△ABC的面积．
如图，在等腰三角形ABC中，两底角的平分线BE和CD相交于点0，则△OBC是