题目内容
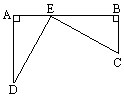
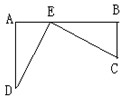
 如图,铁路上A、B两站相距25千米,C、D两村庄视为两点,DA⊥AB于A,CB⊥AB于B,已知DA=15千米,CB=10千米,现要在铁路AB上修一个土特产品收购站E,收购站E到C、D两村庄的距离和最小值为
如图,铁路上A、B两站相距25千米,C、D两村庄视为两点,DA⊥AB于A,CB⊥AB于B,已知DA=15千米,CB=10千米,现要在铁路AB上修一个土特产品收购站E,收购站E到C、D两村庄的距离和最小值为
- A.25千米
- B.10
 千米
千米 - C.25
 千米
千米 - D.5
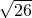 千米
千米
C
分析:根据轴对称求最短路线作出D点对称点D′,连接D′C即可得出E点位置,再利用勾股定理得出CD′即为收购站E到C、D两村庄的距离和最小值.
解答: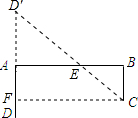 解:作D点关于AB的对称点D′,过点C作CF⊥AD于点F,
解:作D点关于AB的对称点D′,过点C作CF⊥AD于点F,
∵铁路上A、B两站相距25千米,DA=15千米,CB=10千米,
∴FC=25km,D′F=15+10=25(km),
∴CD′=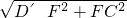 =25
=25 (km).
(km).
故收购站E到C、D两村庄的距离和最小值为:25 km.
km.
故选:C.
点评:此题主要考查了利用轴对称求最短路线问题,根据已知得出E点位置是解题关键.
分析:根据轴对称求最短路线作出D点对称点D′,连接D′C即可得出E点位置,再利用勾股定理得出CD′即为收购站E到C、D两村庄的距离和最小值.
解答:
 解:作D点关于AB的对称点D′,过点C作CF⊥AD于点F,
解:作D点关于AB的对称点D′,过点C作CF⊥AD于点F,∵铁路上A、B两站相距25千米,DA=15千米,CB=10千米,
∴FC=25km,D′F=15+10=25(km),
∴CD′=
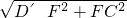 =25
=25 (km).
(km).故收购站E到C、D两村庄的距离和最小值为:25
 km.
km.故选:C.
点评:此题主要考查了利用轴对称求最短路线问题,根据已知得出E点位置是解题关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 如图,铁路上A、B两站相距25千米,C、D两村庄视为两点,DA⊥AB于A,CB⊥AB于B,已知DA=15千米,CB=10千米,现要在铁路AB上修一个土特产品收购站E,收购站E到C、D两村庄的距离和最小值为( )
如图,铁路上A、B两站相距25千米,C、D两村庄视为两点,DA⊥AB于A,CB⊥AB于B,已知DA=15千米,CB=10千米,现要在铁路AB上修一个土特产品收购站E,收购站E到C、D两村庄的距离和最小值为( )