题目内容
用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,第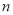 个图形中需要黑色瓷砖__________块(用含
个图形中需要黑色瓷砖__________块(用含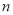 的代数式表示).
的代数式表示).

3n+1
【解析】
试题分析:找出数量上的变化规律,从而推出一般性的结论.
第一个图形有黑色瓷砖3+1=4块.
第二个图形有黑色瓷砖3×2+1=7块.
第三个图形有黑色瓷砖3×3+1=10块.
…
第n个图形中需要黑色瓷砖3n+1块,
故答案为:3n+1.
考点:规律型:图形的变化类.
考点分析: 考点1:整式 (1)概念:单项式和多项式统称为整式.他们都有次数,但是多项式没有系数,多项式的每一项是一个单项式,含有字母的项都有系数.
(2)规律方法总结:
①对整式概念的认识,凡分母中含有字母的代数式都不属于整式,在整式范围内用“+”或“-”将单项式连起来的就是多项式,不含“+”或“-”的整式绝对不是多项式,而单项式注重一个“积”字.
②对于“数”或“形”的排列规律问题,用先从开始的几个简单特例入手,对比、分析其中保持不变的部分及发展变化的部分,以及变化的规律,尤其变化时与序数几的关系,归纳出一般性的结论. 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
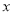 的一元二次方程
的一元二次方程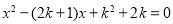 的两个实数根为
的两个实数根为 ,
,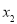 .
.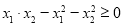 成立?若存在,请求出k值,若不存在,请说明理由.
成立?若存在,请求出k值,若不存在,请说明理由. 左边变成完全平方式后,方程是( )
左边变成完全平方式后,方程是( ) B、
B、 C、
C、 D、
D、
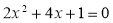 ,配方后的方程是( )
,配方后的方程是( )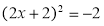 B、
B、
 D、
D、
 =________.
=________. ,并沿东北方向
,并沿东北方向 移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,
移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米, 市位于点
市位于点 的北偏东75°方向上,距离
的北偏东75°方向上,距离 点480千米.
点480千米.
 市;
市;