题目内容
(6分)如图,台风中心位于点 ,并沿东北方向
,并沿东北方向 移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,
移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米, 市位于点
市位于点 的北偏东75°方向上,距离
的北偏东75°方向上,距离 点480千米.
点480千米.

(1)说明本次台风是否会影响 市;
市;
(2)若这次台风会影响 市,求
市,求 市受台风影响的时间.
市受台风影响的时间.
(1)本次台风会影响B市.
(2)B市受台风影响的时间为5小时.
【解析】
试题分析:(1)作BH⊥PQ于点H,在Rt△BHP中,利用特殊角的三角函数值求出BH的长与260千米相比较即可.
(2)以B为圆心,以260为半径作圆交PQ于P1、P2两点,根据垂径定理即可求出P1P2的长,进而求出台风影响B市的时间.

解:(1)作BH⊥PQ于点H.
在Rt△BHP中,
由条件知,PB=480,∠BPQ=75°-45°=30°,
∴BH=480sin30°=240<260,
∴本次台风会影响B市.
(2)如图,若台风中心移动到P1时,台风开始影响B市,台风中心移动到P2时,台风影响结束.
由(1)得BH=240,由条件得BP1=BP2=260,
∴P1P2= =200,
=200,
∴台风影响的时间t= =5(小时).
=5(小时).
故B市受台风影响的时间为5小时.
考点:垂径定理的应用;勾股定理.
考点分析: 考点1:函数基础知识 函数的定义:一般地,在一个变化过程中,如果有两个自变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
对函数概念的理解,主要抓住以下三点:
①有两个变量;
②一个变量的每一个数值随着另一个变量的数值的变化而变化;
③对于自变量每一个确定的值,函数有且只有一个值与之对应。
例如:y=±x,当x=1时,y有两个对应值,所以y=±x不是函数关系。对于不同的自变量x的取值,y的值可以相同,例如,函数:y=|x|,当x=±1时,y的对应值都是1。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
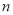 个图形中需要黑色瓷砖__________块(用含
个图形中需要黑色瓷砖__________块(用含

 中,
中, =90°,点
=90°,点 是弧
是弧 上的一个动点(不与点
上的一个动点(不与点 、
、 重合)
重合) ,
, ,垂足分别为
,垂足分别为 、
、 .
.
 时,求线段
时,求线段 的长;
的长; 中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由; ,
, ,求
,求 关于
关于 的函数关系式,并写出
的函数关系式,并写出 的范围.
的范围.
 的方程
的方程 是一元二次方程,则
是一元二次方程,则 的取值是( )
的取值是( )  C.
C. D.
D.

 化成一般形式后,一次项系数和常数项分别为( )
化成一般形式后,一次项系数和常数项分别为( ) B、
B、 C、
C、 D、
D、