题目内容
18．
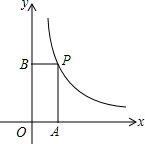如图，在平面直角坐标系中，点P是反比例函数y=$\frac{k}{x}$（x＞0）图象上的一点，分别过点P作PA⊥x轴于点A，PB⊥y轴于点B．若四边形OAPB的面积为3，则k的值为（ ）| A． | 3 | B． | -3 | C． | $\frac{3}{2}$ | D． | -$\frac{3}{2}$ |
分析 因为过双曲线上任意一点引x轴、y轴垂线，所得矩形面积S是个定值，即S=|k|．再由函数图象所在的象限确定k的值即可．
解答 解：∵点P是反比例函数y=$\frac{k}{x}$（x＞0）图象上的一点，分别过点P作PA⊥x轴于点A，PB⊥y轴于点B．若四边形OAPB的面积为3，
∴矩形OAPB的面积S=|k|=3，
解得k=±3．
又∵反比例函数的图象在第一象限，
∴k=3．
故选A．
点评 本题主要考查了反比例函数y=$\frac{k}{x}$中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点；这里体现了数形结合的思想，做此类题一定要正确理解k的几何意义．
练习册系列答案
相关题目
如图，在△ABC中，AB=BC=4，S△ABC=4$\sqrt{3}$，点P、Q、K分别为线段AB、BC、AC上任意一点，则PK+QK的最小值为2$\sqrt{3}$．
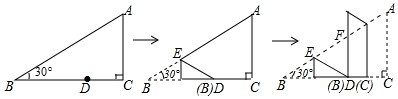
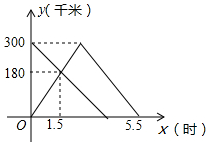甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示．
如图，E，F，G，H分别是矩形ABCD各边的中点，AB=6，BC=8，则四边形EFGH的面积是24．
