题目内容
已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于点D,CE平分∠OCD交⊙O于E.

(1)如图1,求证:
=
;
(2)如图2,若CE=4,求四边形ACBE的面积.

(1)如图1,求证:
 |
| EA |
 |
| EB |
(2)如图2,若CE=4,求四边形ACBE的面积.
分析:(1)首先连接OE,易证得∠OCE=∠E=∠ECD,即可判定OE∥CD,又由垂径定理,即可证得
=
;
(2)首先过点A作AN⊥CE于点N,作BM⊥CE于点M,易证得△AEN≌△EBM,△BCM是等腰直角三角形,继而可得AN+BM=CE,继而求得答案.
 |
| EA |
 |
| EB |
(2)首先过点A作AN⊥CE于点N,作BM⊥CE于点M,易证得△AEN≌△EBM,△BCM是等腰直角三角形,继而可得AN+BM=CE,继而求得答案.
解答:解:(1)连接OE,
∵OE=OC,
∴∠OCE=∠E,
∵CE平分∠OCD交⊙O于E,
∴∠DCE=∠OCE,
∴∠OCE=∠E,
∴OE∥CD,
∵CD⊥AB,
∴OE⊥AB,
∴
=
;

(2)过点A作AN⊥CE于点N,作BM⊥CE于点M,
∵AB为⊙O的直径,
∴∠AEB=∠ACB=90°,
∴∠AEN+∠BEM=∠BEM+∠EMB=90°,
∴∠AEN=∠EMB,
∵CE平分∠OCD,
∴
=
,∠BCM=45°,
∴AE=BE,△BCM是等腰直角三角形,
在△AEN和△EBM中,
,
∴△AEN≌△EBM(AAS),
∴AN=EM,
∴AN+BM=EM+CM=CE=4,
∴S四边形ACBE=S△ACE+S△BCE=
CE•AN+
CE•BM=
CE•(AN+BM)=
CE•CE=
×4×4=8.
∵OE=OC,
∴∠OCE=∠E,
∵CE平分∠OCD交⊙O于E,
∴∠DCE=∠OCE,
∴∠OCE=∠E,
∴OE∥CD,
∵CD⊥AB,
∴OE⊥AB,
∴
 |
| EA |
 |
| EB |

(2)过点A作AN⊥CE于点N,作BM⊥CE于点M,
∵AB为⊙O的直径,
∴∠AEB=∠ACB=90°,
∴∠AEN+∠BEM=∠BEM+∠EMB=90°,
∴∠AEN=∠EMB,
∵CE平分∠OCD,
∴
 |
| AE |
 |
| BE |
∴AE=BE,△BCM是等腰直角三角形,
在△AEN和△EBM中,
|
∴△AEN≌△EBM(AAS),
∴AN=EM,
∴AN+BM=EM+CM=CE=4,
∴S四边形ACBE=S△ACE+S△BCE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了圆周角定理、全等三角形的判定与性质以及等腰直角三角形性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°.
如图,已知AB为⊙O的直径,PA,PC是⊙O的切线,A,C为切点,∠BAC=30°. 22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )
22、如图,已知AB为⊙O的直径,C为⊙O上一点,CD⊥AB于D,AD=9,BD=4,以C为圆心,CD为半径的圆与⊙O相交于P,Q两点,弦PQ交CD于E,则PE•EQ的值是( )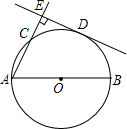 如图所示,已知AB为⊙O的直径,C、D是直径AB同侧圆周上两点,且弧CD=弧BD,过D作DE⊥AC于点E,求证:DE是⊙O的切线.
如图所示,已知AB为⊙O的直径,C、D是直径AB同侧圆周上两点,且弧CD=弧BD,过D作DE⊥AC于点E,求证:DE是⊙O的切线. (2013•沙市区一模)如图,已知AB为⊙O的直径,PA与⊙O相切与点A,线段OP与弦AC垂直并相交于点D,OP与⊙O相交于点E,连接BC.
(2013•沙市区一模)如图,已知AB为⊙O的直径,PA与⊙O相切与点A,线段OP与弦AC垂直并相交于点D,OP与⊙O相交于点E,连接BC. 已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段( )的长.
已知AB为半圆的直径,弦AD、BC相交于M,点E在AM上,且∠CEM=∠B,AB=1,则cos∠AMC的值等于线段( )的长.